Point source and sink in a uniform axisymmetric flow

Placing a point source and/or sink in a uniform horizontal stream of — U leads to very similar results as found in Section 3.3.5 for the two-dimensional case with line sources and sinks.

First the velocity potential and stream function for uniform flow, – U, in the z direction must be expressed in spherical coordinates. The velocity components qR and qv are related to — V as follows

qR = — U cos p and qv = U sin p

Using Eqn (3.60) followed by integration then gives

ф = — V R cos p+f (p) ф = —U R cos p + g(R)

f(p) and g(R) are arbitrary functions that take the place of constants of integration when partial integration is carried out. Plainly in order for the two expressions for ф derived above to be in agreement f(p) — g(R) = 0. The required expression for the velocity potential is thereby given as

ф = —UR cos p

Similarly using Eqn (3.62) followed by integration gives

дф j UR2

— = —U R cos p sin p =——– — sin 2p ■

dp 2

, UR2 ., . ,

Ф =—– sin p + g{p)

Recognizing that cos 2p = 1 — 2 sin2 p it can be seen that the two expressions given above for ф will agree if the arbitrary functions of integration take the values f{R) = —U R2/4 and g(p) = 0. The required expression for the stream function is thereby given as

UR2 . 2

—-— sin p

Using Eqns (3.63) and (3.65) and Eqns (3.64) and (3.66) it can be seen that for a point source at the origin placed in a uniform flow – U along the z axis

2 * 4тг

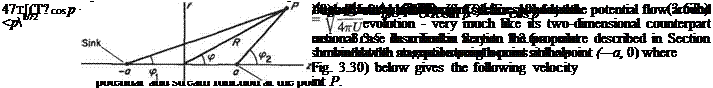(3.67a)

If this source-sink pair is placed in a uniform stream — U in the z direction it generates the flow around a body of revolution known as a Rankine body. The shape is very similar to the two-dimensional Rankine oval shown in Fig. 3.18 and described in Section 3.3.7.