PROPERTIES OF CLASSICAL AND SWEPT AIRCRAFT

4.1 A family of aircraft according to Cayley’s concept. Long before Lilienthal flew his first glider (1891) and the Wright Brothers made the first flight in a powered aircraft (1903), Sir George Cayley thought out the design concept of the classical type of aircraft. In 1799,he gave up the idea of designing aircraft as ornithopters and thus imitating bird flight, which had dominated man’s thinking from the beginning, and replaced it by a concept well – adapted to human engineering: to separate the functions which he identified as essential for achieving flight and to design aircraft to have largely independ­ent organs to fulfil these functions, namely, of providing volume for the pay­load, lift forces, thrust forces, and control forces and moments. These distinct organs can readily be identified as a fuselage, wings, engines, and various control surfaces. Interference effects between them are intended to be essen­tially small. Cayley published his results and proposals in a classical paper in three parts (1809 and 1810) and this laid the foundations of aviation. De­tails about Cayley’s work may be found in С H Gibbs-Smith (1962). There are now good reasons to believe that one of the gliders designed by Cayley was, in fact, flown successfully in 1853 by his "reluctant coachman" (see Anon (1974)).

Conceptually, the classical type of aircraft reached its final form in the streamline aeroplane of Melvill Jones (1929), and this was then extended to the closely related swept-winged type of aircraft by A Betz (1940). Cayley’s design concept has not only replaced the old craving for imitating Nature but it has now been widely accepted as though it was itself a law of Nature and the only possible layout for aircraft. It is only recently that other major types of aircraft have appeared, which utilise different types of flow and, to various degrees, the principle of integrating the functions of several organs, as is generally done in animal flight, but in different ways adapted to human engineering.

On the basis of Cayley’s concept alone, some fundamental properties of the classical subsonic aircraft can be derived. The separation of functions allows us to break down the weight of such an aircraft in a simple manner, to a first order. It also allows us to use a simple relation between lift and drag and to regard the engine thrust as independent of these, again to a first order.

We follow here a performance analysis given by D KUchemann & J Weber (1966).

A first-order weight breakdown has already been described in Section 1.2, and

(1.9) presents the overall weight W of a classical aircraft as the sum of items which are proportional to the overall weight, others which are propor­tional to the payload Wp, and of the engine weight Wg and the fuel weight WF. This breakdown will be retained here, and we shall see later that more detailed considerations do not alter the main conclusions which we shall derive.

A first-order drag relation has already been given in Section 3.2, and (3.42) presents the overall drag of a classical aircraft as the sum of two terms: a friction and form drag, Cpg, which includes the profile drag of the wing as well as friction forces on the other organs, such as the fuselage and the engine nacelles; and a lift-dependent drag, Сщ,, which is predominantly the vortex drag Cjjy of the wing. We have already seen that (3.42) may be

regarded as a good approximation if the wing has a high aspect ratio A, and if the trailing vortex sheet is reasonably flat near the wing, i. e. when

A = 4s2/S = 2s/c » 1 ,

where s is the semispan of the wing, S the area of the wing planform, and "C the mean chord of the wing. That this assumption is consistent with the concept of the classical subsonic aircraft can be seen as follows: the analy­

sis given in Section 1.2 and the relations derived there for the flight range, (1.7), and for the payload fraction, (1.11), indicate that the value of the product npL/D of the propulsive efficiency and the lift-to-drag ratio should reach some value (about тг) so as to give reasonably economic transport aircraft, by (1.12). Now, L/D as determined from (3.42) has a maximum value with respect to CL :

(4.1)

and so this maximum value should reach at least ir/n, which can be taken as about 16 if a typical value of n = 0.2 is assumed for a turbojet engine at a subsonic flight Mach number Mq = 0.7. This means that A should have a minimum value which can be determined from (4.1):

(4.2)

To get some rough indication, we may put Ky * 1.2 and Сщ – 0.02, and so we find that the aspect ratio should be around 7 or more, i. e. we are indeed interested only in classical aircraft which have wings of high aspect ratio. This is an important result which we shall recognise also as the basis of clas­sical aerofoil and wing theory.

At this point, we should check the approximations made so far against some ac­tual values pertaining to a typical subsonic transport aircraft of the present

LIVE GRAPH

Click here to view

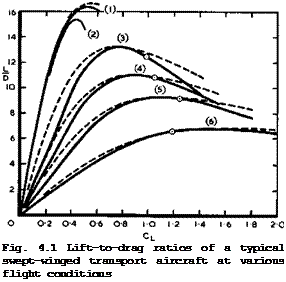
generation for medium ranges. Such an aircraft may have an aspect ratio of about 7 and an angle of sweep of about 35°. Fig. 4.1 shows typical values of L/D for six different flight conditions. The cases are listed in the Table below. Each condition corresponds to a different geometric configuration of

Curve	Configuration	CDF
(1)	cruise	Г low Mach number	0.0165	1.2
(2)		1_ cruise Mach number		—
(3)	low	■ no flap deflection	0.0285	1.1
(4)	speed, leading edge * device	small flap deflection	0.041	1.1
(5)	moderate flap deflection	0.0605	1.05
(6)	in use	. large flap deflection	0.116	1.0

Cases taken for the curves in Fig. 4.1

the aircraft: the wing is "clean" at cruise, but various devices are exten­

ded at the other flight conditions. Strictly, therefore, we are dealing with a variable-geometry aircraft.

In the cruise configuration, values of (L/D)m near 16 are obtained, and the curve labelled (2) shows how the drag rise due to compressibility effects re­duces the value of (L/D)m. A leading-edge device such as a slat, brought into operation at low speeds, curve (3), causes a considerable drop in (L/D)m but shifts it to a higher value of Cl, as desired. The same trend persists when trailing-edge flaps are deflected. The curves (4) and (5) represent typical take-off conditions and (6) the landing approach. One might query why the various high-lift devices reduce the lift-to-drag ratio so much, bearing in mind that the flow can be expected to be attached everywhere, with the excep­tion of case (6) where the flow may well be separated over the flap deflected through about 45°. Here, we can only note that the viscous effects, i. e. both friction and pressure drag, must be relatively large on these multiple aerofoils. We also note that the results given in Fig. 4.1 still imply that there exists a strong overall suction force in the direction of the wing chord (see Section 3.2, (3.30)). If this had vanished, as a result of vis­cous effects, then L/D would have been about 4 at Cl = 1 and about 2 at

Cl = 2 . This does not mean that one could not do better than the results

in Fig. 4.1, and to improve the aerodynamic design of high-lift devices remains an important task.

Fig. 4.1 also gives some indication of how well the simple drag relation (3.42) can represent the actual properties of a complete aircraft. The dashed lines have been worked out from (3.42), choosing values of Cpy and Ky empirically to fit the actual values somewhere near the maximum values of l/d. As

listed in the Table above, we find that the values of Ky can b’e reduced

from about 1.2 for the cruise configuration to about 1.0 for the high-lift configuration in the approach to landing, possibly because the trailing vortex sheet becomes significantly non-planar at the higher lifts in a way which reduces the vortex drag factor. Thus the reductions of the lift-to-

drag ratio are caused by considerable increases in the viscous drag Cpp, emphasising again the need for understanding the viscous effects so that improvements can be attempted. We note further that (3.42) gives a good fit for the cruise configuration, curve (1), with the exception of the very last part of the curve at the higher CL-values. The fit is not quite so good for the low-speed configurations. This indicates some sensitivity to off-design conditions: if the high-lift systems work efficiently near (L/D)m, their

performance deteriorates somewhat at both lower and higher CL-values and, because of non-linear effects, the drag cannot be represented by constant values of Сцр and Ky. On the whole, however, we find that (3.42) is a useful relation for survey purposes.

The next question that arises from such an overall view of the lift and drag forces as shown in Fig. 4.1 is that of where, i. e. at what CL-values, the aircraft will operate under the various flight conditions. Considering only the aerodynamic properties, one would require operation at the maximum value of the lift-to-drag ratio, (L/D)m, but this is not generally acceptable in practice because other considerations must be taken into account. At low speeds, both at take-off and landing,, safety considerations, as defined by the certification authorities, demand that the aircraft should be flown at speeds well above the stalling speed, Vg, which corresponds to the maxi­mum lift obtainable. For example, the speed at take-off should be more than 1.2 Vc; and the approach speed should not be lower than 1.3 Vg. The

curves in Fig. 4.1 end where С^тах, i. e. the stalling speed, is reached

and hence the circles on the curves indicate typical operating conditions.

In a good design, one would aim at having these operating points to coincide with (L/D)m for the particular configuration; it helps that the maximum of the L/D-curve is likely to be fairly flat.

Matters are more complicated when it comes to the choice of a suitable opera­ting condition at cruise. Here, the aim is obviously to make the payload

fraction Wp/W as large as possible and to keep the other weight items down.

To a first order, this is a compromise between the opposing effect of the fuel weight and the engine weight on the payload. It must then be admitted that the aircraft flies at a value of L/D which is below the maximum value, so that, with (3.42) and (4.1),

Since (L/D)m is reached at

the Cl-value at cruise can then be expressed as

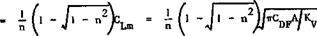C,

Consider now the fuel weight Wp. This can be written as

according to (1.10) where R is the Broguet range. This decreases with in­creasing n, if the aerodynamic and propulsion parameters are regarded as given quantities, i. e. if the configuration of the aircraft is fixed. The lowest fuel fraction Wp/W is then reached when n = 1 .

Consider next the engine weight Wp. Here, we must make several assumptions. We consider the case of turbojet engines and assume that the engine thrust (and hence the weight) is determined by cruise considerations and that the thrust so obtained is then also sufficient to meet the airfield and clind> re­quirements. Further, the engine is assumed to be of the kind where, for a given cruising Mach number, Mcf, and cruising height above the tropopause, hcr, the thrust varies approximately in proportion to the dynamic head

Hence, the engine weight may be assumed to be

Th

‘3!p v2

2 cr cr

C3 is a constant associated with the particular kind of engine chosen.

since Lcr ts W and Th = D in level flight. Using (4.3) and (4.5) we have finally

E = 2c C —__ L (і – 11 – n2 ^ (4.!

W 2 3CDF W/S д2 у */ J ‘

We find that the engine weight shows the opposite trend to the fuel weight and decreases with decreasing n. The function of n in (4.9) decreases from 1 at n = 1 to J at n – 0 . We note also that the engine weight decreases with decreasing zero-lift drag Сцр and with increasing wing loading W/S. But, in the subsequent first-order analysis, the important design parameters Срр and W/S are considered to be constant, as is the value of the factor C3 . All this means in simple terms is that, although

L/D increases with increasing n, the drag itself may also increase and

thus a more powerful and hence heavier engine may be required.

With Wp/W from (4.6) and Wp/W from (4.9), the payload fraction Wp/W can be determined from (1.11), using the general weight breakdown (1.9):

This relation for the payload may be regarded as a function of n for any member of a family of aircraft with given values of C])p, A/Ky, W/S and R as well as cj_, c2 , C3 . A value of n must exist for which the pay­load has a maximum value. This value of n is determined by the relation