Propulsion flow cycles

3.6 We consider now the changes of state of a cer­tain mass of air, or system, between a station 1 just upstream of where energy is supplied and a station 2 just downstream of it. All properties and functions of state of the medium used here are specific values, referred to unit mass. In undergoing a change of state, the flowing air delivers to the

surroundings mechanical energy which can be technically utilised. This energy we shall call the technical work, denoted by w. Mechanical energy may also be delivered to the air from the outside. Since the system considered is the air, this, by our definition, is negative work. To write down an energy balance for a flow process, we must include the kinetic energy e^ » ,

where V is the velocity of the medium, and the heat supplied, q^ • Final­ly, we must include the work done on the medium in state 1 in delivering it across a surface of area S to the region in which the change of state takes place and the work which it does in leaving the region in state 2. To dis­place the gas which is in the surface a distance dx through it, work pjSdx is done, that is, work p^Sdx is done in delivering a mass Sdx/v^ , where v^ is the specific volume (referred to unit mass). Then the work done delivering unit mass is p^Sdxv^/Sdx = p. v^. Similarly, work P2V2 is done by unit mass of air leaving the region. This can be shown to be the specific enthalpy h which, for an ideal gas, can be written as с T, where c_ is the specific heat at constant pressure and T the absolute temperature.

We shall restrict ourselves to ideal gases as these show the main effects we want to consider. This means that the basic functions of state: pressure p, density p, and temperature T, are not independent of one another but obey the equation of state

p = PRT, (3.51)

where R is a characteristic dimensional constant of the gas concerned (for air, R “ 287 m^/s2°K). Altogether, we have for the energy balance between the two states*)

	hl + *kl	+ q12	“ W12 + h2 +	ek2
or	CPT1+ ekl	+ q12	‘ W12 + CpT2	+ ek2	► .	(3.52)
or		d’w	= – dh-dek	+ d’q

This may be called the first law of thermodynamics for flowing media. To be complete, the relation should contain also the changes in potential energy of position, which are ignored here. In some cases, technical work and kinetic energy may conveniently be taken together as the available mechanical energy of the flow:

ea = w + ek. (3.53)

Air enters with kinetic energy and e&^ = ekl" Energy is added by the

thermodynamic process and the available energy of the air is then ea2 = e^ + w.

To describe the flow cycle fully, we must also invoke the second law of thermo­dynamics, which relates to the availability of the energy of a system for con­version into mechanical work. It states the impossibility of converting into

*)

Some of the differentials are primed because neither q nor w is a func­tion of state. The integration of these equations can only be carried out if the path of integration is given, i. e. if the way in which the gas changes from state 1 to state 2 is fixed.

work all the heat supplied to an engine operating on a periodic cycle. The quantitative statement of the law, which we shall need here, defines a func­tion of state, the entropy s. If s^ is the specific entropy of a medium in state 1 and S2 is the specific entropy in state 2, then

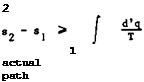where the integral is taken over any reversible path by which state 2 can be reached from state 1. A reversible change 1 -* 2 is defined as a change such that both the system and its surroundings can somehow be restored exactly from state 2 to the original state 1. In an irreversible change, e. g. a process involving friction, the increase in specific entropy of a medium exceeds the value of the integral in (3.54). To include both types of process, we state

where the d’q now refers to the actual heat received in the change of state 1 -*• 2. Reversible and irreversible changes between the same conditions of a

system differ in the changes of entropy of the surroundings. Irreversibility is wasteful in the conversion of energy into mechanical work. All real flow processes are irreversible, but the idea of a reversible process is, neverthe­less, of practical value as a guide to perfection.

Reversible processes may be thought of as brought about by macroscopic motion. It is then conceivable that the process could be reversed and the original state restored. Irreversible changes may be thought of as brought about by microscopic motion. In that case, one cannot see how matters could be organ­ised so as to bring all the particles back to their original positions and states.

The second law of thermodynamics, as expressed in (3.54), is not used in the sense of providing a differential equation, as does the first law; but the second law is necessary to exclude certain processes that satisfy the govern­ing equations but are physically impossible because they lead to a net decrease in entropy.

In building up flat) cycles, we frequently meet some specific changes of state. Some of these are:

1 Isobaric processes, where p = constant, so that for perfect gases which obey (3.51),

p2/pl = Tl/T2 * (3.56)

In this case, the available energy remains constant.

2 Isothermal processes, where T – constant, so that

Pl/pl – P2/P2 •

In this case, all the heat is transformed into available energy.

3 Adiabatic processes, where d’q = 0, so that

c dT – RT dp/p = 0 .

P

Integration gives the well-known relations

pl/p2 = (ti/T2>Y/(Y-1) pl/p2 = (P1/P2>Y f

pl/p2 = (T1/T2)1/(y_1)

where у = Cp/cv is the ratio of the specific heats, which we shall assume to be constant. Certain processes of this kind are isentropic, i. e. s2 ~ S1 = °*

4

If no technical work is done, d’w = 0 , so that

In general, we present the variables in non-dimensional form. Reference values can easily be found in the undisturbed flow upstream of the body.

Those employed are pg, pg, and Vg. RTg is used as reference unit for specific energies. The energy equation (3.60) for perfect gases then reads in non­dimensional form

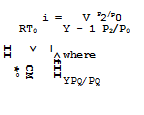
_L_ LL^!2 + Im2

Y – • pj/pg 2 1

introducing the Mach number M (3.62) defines the velocity of sound in the undisturbed flow, used for reference here. There are, of course, various other ways of defining a Mach number and it is often convenient to use the local velocity of sound for reference. Bernoulli’s equation (2.11) is a special form of (3.60) for isentropic flows without heat supply.

We can now proceed to consider some complete flow cycles and begin with some simple cases where we assume that no technical work is done on the surround­ings, i. e. w ■ 0 in (3.52). This is a severe restriction; it implies that changes of state along streamlines in a complete flow pattern in two or three dimensions can be treated as those in a onedimensional flow along a streamtube. Within this restriction, we can use (3.50) and equate the available propulsive work per unit mass, V0(Vj – V0), to the specific thrust work, ThV0. In such a onedimensional treatment, we also ignore how any such changes come about; for example, we assume that heat is added at some station without considering the physical and chemical processes that must be involved. We also ignore any mass addition, e. g. by the fuel. But we can then get some first relations for the efficiencies with which energies can be converted into mechanical work and thus provide some basis for the approximations used in the overall assessment in Section 1.2.

Consider a flow cycle in which heat is supplied at constant pressure in a streamtube with slowly-varying cross-section. This is a fairly realistic case; it can be approached in combustion chambers with diffusion flames. In such a
process between stations 1 and 2,

q12 = q = cp(T2 – Tx) , (3.63)

so that the available energy remains constant by (3.52), i. e.

Леа “ i(V22 “ Vl2) * q12 ‘ cp(T2 " V “ 0 ‘ (3.64)

This means that the velocity does not change during heat addition.

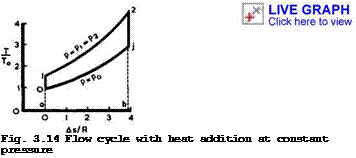
In a T, s-diagram (for obvious reasons, we plot only the changes, As, in en­tropy), Fig.3.14, the process is represented by the isobar between points 1 and 2, and the area al2ba represents the heat input. To obtain something useful, we must add another change of state in the flow downstream of "combustion", in which the available mechanical energy is converted into kinetic energy. This change from state 2 to state j in the jet far downstream can be an expansion without further heat addition:

i(Vj2 " V22) " ~cp(Tj " V • (3.65)

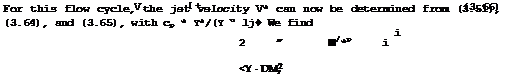We find that the kinetic energy in the jet is the higher the cooler the jet is. This change is accompanied by a fall in pressure and must end on the isobar p * p0 because the pressure far downstream in the jet must be the ambient pres­sure. If no energy losses are involved, this isentropic change is represented by a vertical line 2 -»■ j in the diagram 3.14. It is essential, of course, that the isobar p * p0 lies wholly below the isobar of heat addition, p * plt and this implies that there must be a compression in the flow from p » p0 far upstream to p * p^ at the beginning of combustion, i. e. from 0 ■* 1 in the diagram. This change has again been assumed to be isentropic and without tech­nical work being done. The flow process can now be completed into a oycte by linking conditions far behind with those far ahead by adding a fictitious change of state from j to 0 at constant pressure, during which heat is rejected to the surroundings. This amount of wasted heat is represented by the area aOjba. It can be shown that the continuous flow process and the flow cycle are equivalent as regards the available energy and the total intake and output of energy. In particular, the area 012jO represents the work done on the flow.

In view of (3.63), it is convenient in this case to use Damktthler’s parameter q/СрТф for the nondimensional heat input. Since, for isentropic compressions
and expansions between the same isobars, without technical work being done, the jet temperature ratio is the same as the combustion temperature ratio,

Tj/T0 = T2/Tl • (3.67)

we can express the jet temperature in the form

In this relation, the Mach number is referred to the local velocity of sound. We then find

This states that V- > Vq, and hence that a thrust force according to (3.50) can indeed be obtained, as soon as q > 0. But V – > Vq and T. > Tq also mean that energy in the forms of kinetic energy and of heat is lefi behind in the stream so that the generation of a thrust force must be paid for.

To measure how efficiently the heat input q is converted into available thrust work Vq(Vj – Vq), an overall propulsive efficiency can be defined:

This is the same propulsive efficiency which appears in Brdguet’s range equa­tion (1.7), multiplied by H, the calorific value of the fuel. Now,

q “ pH, (3.71)

where p is the ratio between the mass of fuel and the mass of air used in the combustion process. Hence,

This quantity should be as large as possible, which implies that the fuel-to – air ratio p should be as small as possible, that is, we want to burn lean mixtures.

It is convenient to split up the overall propulsive efficiency into two compo­nents, one mechanical and the other thermal, so that

The get efficiency гц, or Froude efficiency, measures the available propul­sive work in the jet in terms of the kinetic energy lost in the jet:

The thermal efficiency nth measures the kinetic energy in the jet in terms

of the heat input:

(3.74) together with (3.50)lead to an important conclusion: a given value of the actual thrust Th is generated most efficiently if the largest possible mass of air is captured and then subjected to the flow cycle with energy addi­tion. Further, the backward acceleration should be as small as possible and hence the jet velocity Vj should be as close as possible to the velocity Vq of the mainstream. We have reached similar conclusions in Section 3.1 with regard to the generation of lift forces, in that the largest possible mass of air should be given the smallest downward acceleration to generate the requi­red lift. However, as in that case, aircraft design does not require us to achieve the absolute optimum but only the best within a given set of constrai­nts and of other given quantities. In the present case of propulsion, there are many constraints imposed by the design of the airframe. One of these is the massflow through the propulsion device and hence its size, which must evi­dently be restricted by geometrical and structural considerations. We note, therefore, that the design of a propulsion system is quite inseparable from the design of the aircraft as a whole.

In the case of constant-pressure combustion discussed above, Vj and Tj from (3.69) and (3.68) can be inserted into (3.74) and (3.75) and the component ef­ficiencies determined. With (3.67), the thermal efficiency is simply

Thus the thermal efficiency increases with increasing pressure ratio or increa­sing temperature ratio. This can readily be seen also from the diagram in Fig. 3.14: if the isobar 12 is shifted to higher pressures, the heat input is us­ed to better effect. (3.77) states, in particular, that ntjj increases strong­ly with increasing flight Mach number and approaches unity for infinite Mach number, if the Mach number at the beginning of combustion is kept constant.

This trend is general and not restricted to constant-pressure flow cycles only; it is the basis for Fig. 1.1 and for the assessment given in Section 1.2.

The thermal efficiency (3.76) of the constant-pressure cycle bears a formal re­semblance to that of the hypothetical Carnot cycle. This is built up of an isentropic compression 0 1, a supply of heat at constant temperature Tj,

1 •> 2, an isentropic expansion 2 -»• 3, and a rejection of heat at the con­

stant temperature T3 = Tq of the surroundings. The thermal efficiency is then given by (3.76), but Tj is now the highest temperature reached during the cycle, whereas T2 > T^ in the constant-pressure cycle. A Carnot cycle with T2 as the highest temperature would clearly have a higher efficiency than that given by (3.76). What matters here is that the constant-pressure flow cycle rejects the heat at too high a temperature and hence wastes more
energy during the absorption and delivery of heat, where differences in temp­erature occur between the source of heat and the working medium. This emphas­ises the importance of the maximum temperature reached in a cycle; it must also be one of the main engineering constraints in an actual engine.

The Carnot cycle is important in that it sets a standard, because the exergy of heat can be reached, i. e. the maximum work that can be done by a system when it is brought into equilibrium with its surroundings by reversible changes of state (see e. g. E Schmidt et аЪ. (1975)). It has been striven for by many as an ideal for a long time, but it was found very difficult to see how heat could be added to an actual flow, or subtracted from it, at a constant tempera­ture. Its realisation has been one of the goals of engineers ever since Carnot drew attention to the favourable properties of this cycle in 1824. It was only recently that E G Broadbent & L H Townend (1969) showed that, in principle, this goal oan be reached by an expanding and accelerating flow in which heat is added along a falling pressure gradient. Their analysis applies to a whole class of flows that have a certain kinship with the Prandtl-Meyer expansion. This arises from the fact that it is a turning flow around a corner and that, in cylindrical coordinates with the axis in the direction of no variation, the physical properties depend only on the turning angle ф and not on the radius r. A typical result of their analysis is shown in Fig. 3.15. The mainstream Mach number is Ho * 1 (which is not now a special case as in a Prandtl – Meyer expansion) and the flow is unheated up to ф – ф0 = 0.564. Thereafter, heat must be distributed in a precisely-specified manner in order to preserve isothermal conditions. A few streamlines are shown and a number of radii are labelled with the local values of the Mach number M, the pressure ratio р/р. and a parameter Q defining the heat addition per unit volume 0

<}(г, ф)

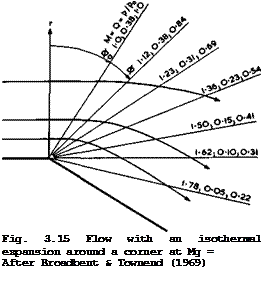where q is the local heat addition per unit mass. Although q varies inversely with r for ф fixed, Q is found to depend only on ф. This would

seem to be quite a realistic flow pattern which could have practical applica­tions in combustion chambers, or in afterburners or in base flows with com­bustion. What remains to be solved are the many problems of fuel injection, mixing, and chemical reactions in the combustion process.

Other attempts to approach the ideal have been concerned with the introduct­ion of heat exchangers into the cycle, without changing the pressures of the working medium and the temperatures of the heat sources. In principle, these heat exchangers pick up heat at the downstream end of the cycle, which would otherwise be rejected to the surroundings, and then move to the upstream end of the cycle to give the heat to the flow there. But the technical difficul­ties to be overcome are considerable, and there is as yet no such engine in the air.

Returning to flow cycles with cons tant-^pres sure combustion, we can determine the overall propulsive efficiency from (3.70) and (3.69) or (3.66) and work out some actual values when we apply the practical constraint that the maxi­mum temperature T2 in the flow should be limited. In the numerical examples given, we put T2/T0 $ 10, to indicate also that such effects as dissocia­

tion of the air should be excluded since this would, in general, lead to further energy losses from the working fluid and invalidate the relations used. Writing the thermal efficiency from (3.76) in the form

we find that the heat input

must be kept low if nth to be reasonably high and if the maximum tempera­ture is prescribed. It must, in fact, be kept well below that of combustion of hydrogen, say, at the stoichiometric mixture, where q/cpTQ is about 15. Thus, as has been concluded before, one of the design aims is to bum tean mixtures for the sake of keeping the engine reasonably cool without a severe penalty in thermal efficiency. Since the size of the engine is also restrict­ed in practice, we are led to include in our considerations flow cycles where the mass flow of air per unit time through the engine is high. This means that the Mach number at the beginning of heat addition may have to be

supersonic in many cases.

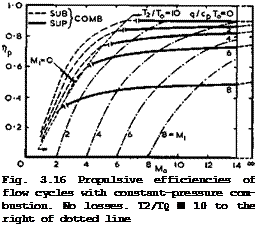
Some numerical results are shown in Fig. 3.16. It is indicated where combus­tion is subsonic and where it is supersonic. This can easily be determined since the Mach number at the beginning of combustion, M^ , depends only on Mq and Tj and hence on nth (or on T2/T0 and q/cpTo):

by the energy equation for perfect gases. Hence M^ > 1 when

„2 > ‘ * ГН "th

– "th

LIVE GRAPH

Click here to view

Means for Generating Lift and Propulsive Forces

We conclude that ёгШвопго or supersonic combustion is not a matter for debate; it simply follows that, if a certain thermal efficiency is desired in a constant-pressure-combustion flow cycle, then combustion is supersonic above a certain flight Mach number. To illustrate this by a numerical example, nth 85 0.8 when Mi2 ■ 0.2Mq2 – i. e.

MX *	0	1	1.8	2.4	3.0	3.5	4.0
Mo =	4.47	5	6	7	8	9	10

If, at the same time, T2/T0 is restricted to 10, then Ti/Tq * 5 and q/cpT0 e 5 by 0.79). The ideal inflow pressure ratio is then Pi/po = 280 , which is a very high value by comparison with what can be achieved by mechani­cal means, such as compressors. From the results in Fig. 3.16, we might state that we should investigate further the range of flight Mach numbers between about 5 and 12 and the range of combustion Mach numbers between about 2 and 6 . Most of this work still remains to be done. These matters will be

discussed further in Section 8.5.

In Fig. 3.16, T2/T0 = 10 everywhere to the right of the dotted line. To the left of this, the ram pressure obtained in the inflow streamtube is not high enough to reach this temperature with the specified heat inputs, even though Mi has arbitrarily been put to zero. These cases are thus typical of what may be described as subsonic ramjets. Their propulsive efficiency falls rapidly with decreasing Mach number. This is partly because the compression ratio is becoming too low; and partly because the jet velocity increases and the Froude efficiency, nj, falls. Near Mq = 2 , even the ideal efficiency is no better than the actual propulsive efficiency of existing turbojet engines. Ramjet engines with supersonic combustion, or scramjets, come into their own at higher flight Mach numbers. It is interesting to note again that both the turbojet at low Mach numbers and the scramjet at high Mach numbers want a high excess of air in the combustion process, but for different reasons: in the

turbojet, this improves the Froude efficiency (and high-bypass engines are desirable in this respect); in the scramjet, this keeps the maximum tempera­ture within given limits for a given value of the thermal efficiency.

On the right of the dotted line in Fig. 3.16, and especially in the range of supersonic combustion, the Froude efficiency is generally quite good, which can be seen by comparing the actual values of Пр ■ nth ^j with the scale for nth

on the righthand side, which applies to the whole of the region to the right of the dotted line, where T2/T0 = 10. What matters there is primarily the mixture ratio and the proper coupling of flight Mach number and combustion Mach number.

Although the values shown in Fig. 3.16 refer to an ideal and simple flow cycle, they are certainly not so remote from reality that they could not serve as potential guidelines. The striking improvements with flight speed, in particu­lar, are based on simple physical arguments and therefore set a realistic aim for the future.

We must remenber that the numerical values in Fig. 3.16 refer to a series of different propulsion systems, designed for different Mach numbers. The charac­teristics of a given engine and the actual amount of fuel required to pro­pel a given aircraft at a given altitude and speed depend not only on the flow cycle of the air taking part in the combustion process but also on the proper­ties of the whole flowfield past the lifting propulsive body. Further, they depend on the total thrust needed and hence on the size of the combustion unit relative to the size of the body. Thus the design of any real propulsion system will require a careful and complex matching procedure, and general state­ments about the engine characteristics cannot readily be made. But we can say that, for an engine of given size and thermodynamic flow cycle, we would not want to keep the mass flow through the engine constant with speed and altitude. If we did, Vj would remain constant and the thrust would fall off with in­creasing speed, according to (3.50). Instead, we might aim at approaching a constant-volume flow, in which case V^/Vq would decrease with speed and Pl/p0 increase so that ntu from (3.77) would improve and Vj/Vq increase, according to (3.69). The tnrust could then be kept approximately constant with speed, although it would still fall with altitude. These are possibilities which can be exploited in propulsion systems with flow cycles – other systems are much more restricted.

We must also remember that the numerical values in Fig. 3.16 apply to an ideal flow cycle with constant-pressure combustion and no energy losses other than the heat rejected to the surroundings. There are many other possible sources of energy loss, and these will lower the propulsive efficiency. Before we can assess these, we must discuss in some more detail the flowfields which are associated with the flow cycles and also how thrust forces can be generated and where they can act.