Steady Maneuvers

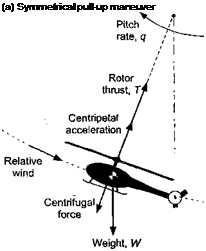
For steady (nontransient) maneuvers, the forces acting on the helicopter can be assumed to act in equilibrium. A classic problem is a level banked turn, which is considered by Saunders (1975) and Prouty (1986). By assuming the helicopter to act as a point mass, the centripetal acceleration required to perform a turn with a flight path of radius Rtum will be V^//?tum, where Too is the true airspeed. With reference to Fig. 5.40(a), the rotor thrust required must overcome both weight W and centrifugal force Fqf giving

This result, of course, assumes that the tail rotor makes a negligible contribution to the problem. The load factor on the rotor is, therefore,

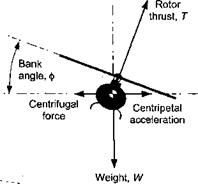
where n is the rotor load factor (n = 1 in level, unaccelerated flight) and g is acceleration under gravity. The bank angle required [refer to Fig. 5.40(b)] will be

ф = cos-1 (1/n) (5.106)

and so for equilibrium the rotor thrust, T, is

T = W/cos(p. (5.107)

These equations allow the rotor thrust to be determined, albeit approximately, for any bank angle and, therefore, for any turning radius of the flight path. Notice that the bank angle required to perform a given radius of turn will also be a function of the speed of the helicopter along its flight path, which is a key factor in determining the load factor for a given radius of turn.

(b) Steady turn

Figure 5.40 Forces acting on a helicopter in (a) a symmetrical pull-up maneuver and, (b) a coordinated tum.

The power required in turning flight with bank angle ф can be determined using the performance model based on momentum theory, as described in Section 5.4. In coefficient form, the total power can now be written as

where CpTR is the contribution from the tail rotor.[21] Notice that it is only the induced part of the power (the thrust dependent term) that is affected by the bank angle, ф, assuming that the tum is coordinated and there is no slip (yaw) angle. For modest bank angles, say up to ф = 30°, there are only mild effects on power requirements. However, for steep bank angles the power required may exceed that available and the maneuver capability could be power limited. This is particularly apparent at high density altitudes, where maneuver performance will almost certainly be limited because of either reduced excess power available or by reaching rotor stall limits. Roll rate (or pitch rate for that matter) has only a secondary and transient effect on rotor power required because rate affects primarily the distribution of thrust over the rotor disk and not its magnitude.