SUPERPOSITION OF A THREE – DIMENSIONAL DOUBLET AND FREE STREAM: FLOW AROUND A SPHERE

The method of the previous section can be extended to study the case of the three-dimensional flow over a sphere. The velocity potential is obtained by the superposition of the free stream potential of Eq. (3.51) with a doublet pointing in the negative x direction (Eq. (3.34)). The combined velocity potential is

(3.114)

(3.116)

1 ЭФ r sin в дер

At the sphere surface, where r = R, the zero normal flow boundary condition is enforced (qr = 0),

4r = (cL – ^3) cos 0 = 0 (3.118)

This condition is met at 0 = я/2, Зя/2 and in general, when the quantity in the parentheses is zero. This second condition is used to determine the doublet strength,

H = Ua*R3 (3.119)

which means that qT = 0 at r = R, which is the radius of the sphere. Substituting the strength p into the equations for the potential and the velocity components results in the flowfield around a sphere with a radius R:

Ф = f/oo cos d(r +	(3.120)
/ R3 q, = cos 0^1 —	(3.121)
/ R* qe = sin 0^1 + ^5)	(3.122)

To obtain the pressure distribution over the sphere, the velocity components at r = R are found:

qr = 0 qe = -|f/» sin 0 (3.123)

The stagnation points occur at 0 = 0 and 0 = я, and the maximum velocity at 0 = я/2 or 0 = Зя/2. The value of the maximum velocity is which is smaller than in the two-dimensional case.

The pressure distribution is obtained now with Bernoulli’s equation

p – p=o = – 4 sin2 0)	(3.124)
and the pressure coefficient is
c’-w=(1-?sin! e) 2PVoc,	(3.125)

It can be easily observed that at the stagnation points 0 = 0 and я (where q = 0) Cp = 1. Also the maximum velocity occurs at the top and bottom of the sphere (в = я/2, Зя/2) and the pressure coefficient there is —5/4.

Because of symmetry, lift and drag will be zero, as in the case of the flow over the cylinder. However, the lift on a hemisphere is not zero (even without introducing circulation); this case is of particular interest in the held of road-vehicle aerodynamics. The flow past a sphere can be interpreted to also represent the flow past a hemisphere on the ground since the x axis is a streamline and can be replaced by a solid surface.

The lift force acting on the hemisphere’s upper surface is

p„o) sin 0 sin <p dS

and the surface element dS on the sphere is

dS = (R sin 0 dq>){R dd)

Substituting dS and the pressure from Eq. (3.124), the lift of the hemisphere is

L = – f f 2P^(1 _ 4 sin2 sin2 0 sin qj dd dcp Jo Jo

= – Ipulf (1 – 3 Sin2 0)2R2 sin2 0 de = – PR2Ui – ^) = %npR2Ul

(3.127)

The lift and drag coefficients due to the upper surface are then

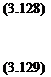L 11

8

D

PUI lR2

For the complete configuration the forces due to the pressure distribution on the flat, lower surface of the hemisphere must be included, too, in this calculation.