THE BASIC LONGITUDINAL FORCES

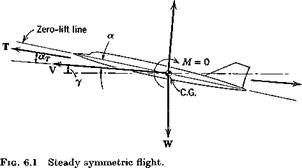
The basic flight condition for most vehicles is symmetric steady flight. In this condition the velocity and force vectors are as illustrated in Fig. 6.1.

The steady-state condition was fully described in Sec. 5.9. All the nonzero forces and motion variables are members of the set defined as “longitudinal” in Chapter 5, and hence we see the central importance of longitudinal aerodynamics. The two main aerodynamic parameters of this condition are

V and a.

Nothing can be said in general about the way the thrust vector varies with

V and a, since it is so dependent on the type of propulsion unit—rockets, jet, propeller, or prop-jet. Two particular idealizations are of interest, however,

(i) T independent of V, i. e. constant thrust; an approximation for rockets and pure jets.

(ii) TV independent of V, i. e. constant power; an approximation for reciprocating engines with constant-speed propellers.

The variation of steady-state lift and drag with a for subsonic and supersonic Mach numbers (M < about 5) are characteristically as shown in Fig. 6.2 for the range of attached flow over the surfaces of the vehicle (refs. 6.5, 6.6). Over a useful range of к (below the stall) the coefficients are given accurately

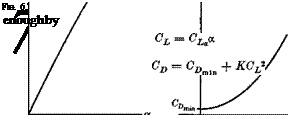The three constants Gl* CnmiI , К are principally functions of the con­figuration shape, thrust coefficient, and Mach number.

Significant departure from the above idealizations may, of course, he anticipated in some cases. The minimum of CD may occur at a value of a > 0, and the curvature of the CL vs. a relation may be an important consideration for flight at high CL. When the vehicle is a “slender body,” e. g. a slender delta, or a slim wingless body, the CL curve may have a characteristic upward curvature even at small a (ref. 6.7). The upward curvature of CL at small a is inherently present at hypersonic Mach numbers (ref. 6.8). For the nonlinear cases, a suitable formulation for CL is (ref. 6.9)

Gl = UCn. sin 2a + CNaa sin a |sin a|) cos a (6.1,3)

where CNa and GNaa are coefficients (independent of a) that depend on the Mach number and configuration. [Actually CN here is the coefficient of the aerodynamic force component normal to the wing chord, and CN is the value of CLa at a = 0, as can easily be seen by linearizing (6.1,3) with respect to a.] Equation (6.1,2) for the drag coefficient can serve quite well for flight dynamics applications up to hypersonic speeds (M > 5) at which theory indicates that the exponent of CL decreases from 2 to ■§. Miele (ref. 6.10) presents in Chapter 6 a very useful and instructive set of typical lift and drag data for a wide range of vehicle types, from subsonic to hypersonic.