UNSTEADY MOTION OF A TWO – DIMENSIONAL THIN AIRFOIL
As is indicated in Section 13.6, steady-state flow methods can be extended to treat the time-dependent problem with only a few modifications. Following this methodology, the time-dependent equivalent of the small disturbance, thin,
|
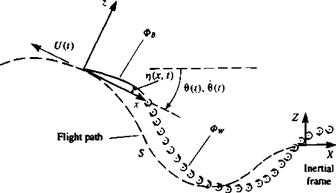
FIGURE 13.14 Nomenclature for the unsteady motion of a two-dimensional thin airfoil (note that the motion is observed from the X, Z coordinate system and the airfoil moves toward the left side of the page). |
lifting airfoil in steady flow (Sections 5.2-5.4) is treated in this section. One of the more difficult aspects of this unsteady problem is the modeling of the vortex wake’s shape and strength, which depends on the time history of the motion. By selecting a discretized vortex wake model at the early stages of this discussion we limit ourselves mostly to numerical solutions. But it seems that this approach allows for a simple formulation (which is clear and easy to explain to students) that avoids an elaborate mathematical treatment of the wake-influence integral.
The two-dimensional, thin lifting surface with a chord length of c is shown schematically in Fig. 13.14. At t = 0 the airfoil is at rest in the inertial system X, Z, and at f>0 it moves along a time-dependent curved path, S. (Note that the fluid in Fig. 13.14 is basically at rest and the airfoil moves toward the left of the page!) For convenience, the coordinates x, z are selected such that the origin is placed on the path S, and the x coordinate is always tangent to the path. The airfoil shape (camberline) is given in this coordinate system by ij(jc, f), which is considered to be small {rj/c « 1). Since small-disturbance motion is assumed, the path radius of curvature g is also much larger than the chord c (or c/g = dc/U(t)« 1).