Viscous Effects in Aerodynamic Flows

This chapter will examine the changes in an aerodynamic flow caused by the presence of viscous wall boundary layers and trailing wakes. The objective is to model and quantify these changes and to explain their associated phenomena such as loss of lift at stall.

3.1 Inviscid Flow Model

Lumping of the vorticity in the viscous layers into vortex sheets, as illustrated in Figure 2.12 in Chapter 2, produces a fictitious strictly-potential Equivalent Inviscid Flow (EIF) velocity field u;, v;(s, n). The EIF also has a pressure field pi(s, n) related to u;, v; by the Bernoulli equation (1.109).

Pi(s, n) = p^ + ^pv* – ^p(u?+vf) (3.1)

Here u, v will denote velocity components along the local orthogonal sheet coordinates s, n.

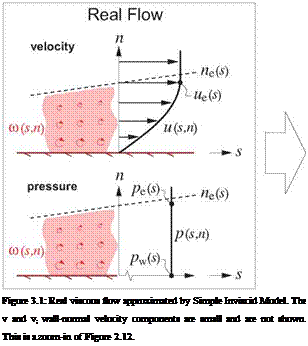
Figure 3.1 compares the EIF to the real flow in more detail, for the case where the lumped vortex sheet is placed on the real surface. It is labeled “Simple” to distinguish it from the more advanced and accurate models considered later, which mostly eliminate the modeling discrepancies in the velocity and pressure in

(3.2)

The subscript ()e will in general denote an “edge” quantity in the irrotational flow just outside the edge of viscous layer, which is demarked by the ne(s) curve shown in Figure 3.1. The subscript ()w will denote a wall quantity at n = 0.

If the boundary layer is thin the vorticity-lumping procedure will incur little error, in which case the wall velocity of the EIF closely approximates the edge velocity of the real flow.

Uiw (s) – Ue(s)

Combining (3.1),(3.2),(3.3) we have

Piw (s) – Pw(s) (3.4)

so that the EIF captures the real surface pressures, and hence should produce reasonably accurate lift forces and moments. Of course the EIF cannot represent the viscous skin friction in the real flow, so that it cannot correctly predict the drag. This will be addressed in Chapter 4.

Although the above discussion assumed incompressible flows, the EIF concept and flow models can be applied to compressible flows. The only differences are that the compressible Bernoulli relation (1.112) would be used in lieu of (3.1), and a grid method would be used in lieu of the vortex-sheet EIF model shown in Figure 3.1.