Circulation and lift (Kutta-Zhukovsky theorem)

In Eqn (3.52) it was shown that the lift / per unit span and the circulation Г of a spinning circular cylinder are simply related by

l = pVT

where p is the fluid density and V is the speed of the flow approaching the cylinder. In fact, as demonstrated independently by Kutta[12] and Zhukovsky*, the Russian physi­cist, at the beginning of the twentieth century, this result applies equally well to a cylinder of any shape and, in particular, applies to aerofoils. This powerful and useful result is accordingly usually known as the Kutta-Zhukovsky Theorem. Its validity is demonstrated below.

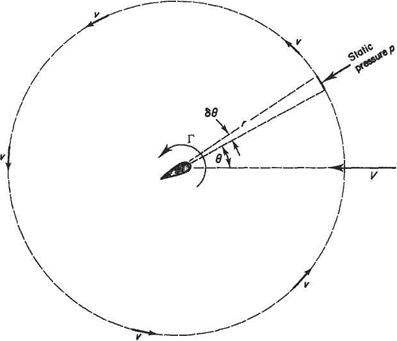
The lift on any aerofoil moving relative to a bulk of fluid can be derived by direct analysis. Consider the aerofoil in Fig. 4.7 generating a circulation of Г when in a stream of velocity V, density p, and static pressure po. The lift produced by the aerofoil must be sustained by any boundary (imaginary or real) surrounding the aerofoil.

For a circuit of radius r, that is very large compared to the aerofoil, the lift of the aerofoil upwards must be equal to the sum of the pressure force on the whole periphery of the circuit and the reaction to the rate of change of downward momen­tum of the air through the periphery. At this distance the effects of the aerofoil thickness distribution may be ignored, and the aerofoil represented only by the circulation it generates.

Fig. 4.7

The vertical static pressure force or buoyancy 4 on the circular boundary is the sum of the vertical pressure components acting on elements of the periphery. At the element subtending 66 at the centre of the aerofoil the static pressure is p and the local velocity is the resultant of V and the velocity v induced by the circulation. By Bernoulli’s equation

Po+jpV2 =p + jp[V2 + v2 + 2Fvsin 6]

giving

p = po – pVvsin#

if v2 may be neglected compared with V2, which is permissible since r is large.

The vertical component of pressure force on this element is

—pr sin 6 66

and, on substituting for p and integrating, the contribution to lift due to the force acting on the boundary is

л2тг

k = ~ (po – pFvsin6)rsin 6d6

Jo (4.7)

+pVvnr

with po and r constant.

The mass How through the elemental area of the boundary is given by pVr cos ObO. This mass flow has a vertical velocity increase of v cos 9, and therefore the rate of change of downward momentum through the element is —pVvr cos2 9b9 therefore by integrating round the boundary, the inertial contribution to the lift, /j, is

/і = + / /э Kit cos2 9d9

J о

= pVvrTT

Thus the total lift is:

I = 2pVvrir

From Eqn (4.5):

2nr

giving, finally, for the lift per unit span, /:

I = pVT

This expression can be obtained without consideration of the behaviour of air in a boundary circuit, by integrating pressures on the surface of the aerofoil directly.

It can be shown that this lift force is theoretically independent of the shape of the aerofoil section, the main effect of which is to produce a pitching moment in potential flow, plus a drag in the practical case of motion in a real viscous fluid.