Circulation and vorticity

From the discussion above it is evident that circulation and vorticity, introduced in Section 2.7, are key concepts in understanding the generation of lift. These concepts are now explored further, and the precise relationship between the lift force and circulation is derived.

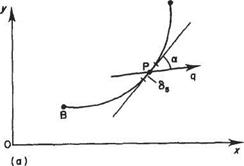
Consider an imaginary open curve AB drawn in a purely potential flow as in Fig. 4.3a. The difference in the velocity potential ф evaluated at A and В is given by the line integral of the tangential velocity component of flow along the curve, i. e. if the flow velocity across AB at the point P is q, inclined at angle a to the local tangent, then

Фа — Фв = Я cos a ds (4.1)

J AB

which could also be written in the form

Фа~Фв= {udx+vdy)

J AB

Equation (4.1) could be regarded as an alternative definition of velocity potential.

Consider next a closed curve or circuit in a circulatory flow (Fig. 4.3b) (remember that the circuit is imaginary and does not influence the flow in any way, i. e. it is not a boundary). The circulation is defined in Eqn (2.83) as the line integral taken around the circuit and is denoted by Г, i. e.

Fig. 4.3 (a) An open curve in a potential flow, (b) A closed curve in a circulatory flow; A and В coincide

Г = cos ads or T = j>(udx + vdy) (4.2)

It is evident from Eqns (4.1) and (4.2) that in a purely potential flow, for which Фа must equal фв when the two points coincide, the circulation must be zero.

Circulation implies a component of rotation of flow in the system. This is not to say that there are circular streamlines, or that elements of fluid are actually moving around some closed loop although this is a possible flow system. Circulation in a flow means that the flow system could be resolved into a uniform irrotational portion and a circulating portion. Figure 4.4 shows an idealized concept. The implication is that if circulation is present in a fluid motion, then vorticity must be present, even though it may be confined to a restricted space, e. g. as in the core of a point vortex. Alternatively, as in the case of the circular cylinder with circulation, the vorticity at the centre of the cylinder may actually be excluded from the region of flow con­sidered, namely that outside the cylinder.

4 t*

Fig. 4.4

Consider this by the reverse argiunent. Look again at Fig. 4.3b. By definition the velocity potential of C relative to A (^ca) must be equal to the velocity potential of C relative to В (фсъ) in a potential flow. The integration continued around ACB gives

Г = Фса ± Фсъ = 0

This is for a potential flow only. Thus, if Г is finite the definition of the velocity potential breaks down and the curve ACB must contain a region of rotational flow. If the flow is not potential then Eqn (ii) in Section 3.2 must give a non-zero value for vorticity.

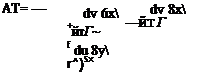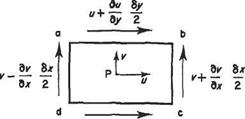
An alternative equation for Г is found by considering the circuit of integration to consist of a large number of rectangular elements of side 6x 6y (e. g. see Section 2.7.7 and Example 2.2). Applying the integral Г = J (u dx + v dy) round abed, say, which is the element at P(x, y) where the velocity is и and v, gives (Fig. 4.5).

The sum of the circulations of all the areas is clearly the circulation of the circuit as a whole because, as the ДГ of each element is added to the ДГ of the neighbouring element, the contributions of the common sides disappear.

Applying this argument from element to neighbouring element throughout the area, the only sides contributing to the circulation when the ATs of all areas are summed together are those sides which actually form the circuit itself. This means that for the circuit as a whole

This shows explicitly that the circulation is given by the integral of the vorticity contained in the region enclosed by the circuit.

bu by U~ by Y

Fig. 4.5

If the strength of the circulation Г remains constant whilst the circuit shrinks to encompass an ever smaller area, i. e. until it shrinks to an area the size of a rectangular element, then:

Г = £ x 6x 6y = £ x area of element

area—*o area of circuit

Therefore,

Here the (potential) line vortex introduced in Section 3.3.2 will be re-visited and the definition (4.2) of circulation will now be applied to two particular circuits around a point (Fig. 4.6). One of these is a circle, of radius r, centred at the centre of the vortex. The second circuit is ABCD, composed of two circular arcs of radii r and r2 and two radial lines subtending the angle (3 at the centre of the vortex. For the concentric circuit, the velocity is constant at the value

C

where C is the constant value of qr.

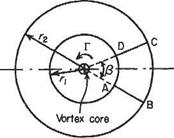
Fig. 4.6 Two circuits in the flow around a point vortex

Since the flow is, by the definition of a vortex, along the circle, a is everywhere zero and therefore cos a = 1. Then, from Eqn (4.2)

Now suppose an angle в to be measured in the anti-clockwise sense from some arbitrary axis, such as OAB. Then

dj = rid#

whence

f2irC

Г = – nd# = 2TrC

Jo r і

Since C is a constant, it follows that Г is also a constant, independent of the radius. It can be shown that, provided the circuit encloses the centre of the vortex, the circulation round it is equal to Г, whatever the shape of the circuit. The circulation Г round a circuit enclosing the centre of a vortex is called the strength of the vortex. The dimensions pf circulation and vortex strength are, from Eqn (4.2), velocity times length, i. e. L2T- , the units being m2 s-1. Now Г = 27гС, and C was defined as equal to qr hence

Г = 2-irqr and

Г

2жг

Taking now the second circuit ABCD, the contribution towards the circulation from each part of the circuit is calculated as follows:

(i) Radial line AB Since the flow around a vortex is in concentric circles, the velocity vector is everywhere perpendicular to the radial line, i. e. a = 90°, cos a = 0. Thus the tangential velocity component is zero along AB, and there is therefore no contribution to the circulation.

(ii) Circular arc BC Here a = 0, cos a — 1. Therefore

(iii)

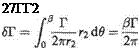Radial line CD As for AB, there is no contribution to the circulation from this part of the circuit.

(iv)

Circular arc DA Here the path of integration is from D to A, while the direction of velocity is from A to D. Therefore a = 180°, cos a = — 1. Then

Therefore the total circulation round the complete circuit ABCD is

(4.6)

Thus the total circulation round this circuit, that does not enclose the core of the vortex, is zero. Now any circuit can be split into infinitely short circular arcs joined by infinitely short radial lines. Applying the above process to such a circuit would lead to the result that the circulation round a circuit of any shape that does not enclose the core of a vortex is zero. This is in accordance with the notion that potential flow is irrotational (see Section 3.1).