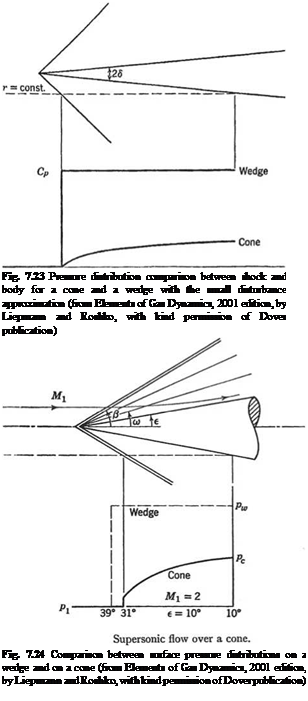
Conical Flow Past a Delta Wing

In general, in a conical flow, all fluid properties are invariant along rays through a common vertex. An example of such flows is a triangular wing in supersonic flow, where disturbances are propagated only in the downstream Mach cone. Notice conical flows are not possible in subsonic flow regime.

Following Shapiro [31] and Ashley and Landhal [1], the governing perturbation potential equation is given by

Fig. 7.25 Delta wing in supersonic flow	y
2 d2ф д2ф д2ф M0)dX2 + – 0
(7.152)
(1

where the origin is placed at the vertex, and the free stream is in the x-direction, Fig. 7.25.

The velocity components (u, v, w) are also governed by similar equations. Following Hayes [27] and Stewart [32], conical coordinates are introduced where

The governing equation for the u-velocity component becomes (see also Ashley and Landhal [1])

2 д2U 1 2 дU 1 д2U

(1 – a 2)^ + a(1 – 2a V + a^ ^ — 0

In the (n, Z) plane. the Mach cone is represented by a unit circle and the wing by a slit along the n-axis of length 2д — в/tan Л, where Л is the sweep angle.

On the mach cone, u, v, w vanish and on the slit w — —a. Using Chaplygin’s transformation, where

1 — V1 — a2 d q 1 q

a ’ d a 1 — a 2 a

the above equation is reduced to the standard, two dimensional Laplace equation

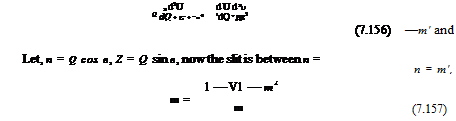
The velocity components are related through the irrotationality conditions, hence on the slit

= 0, |nl < ml (7.158)

dZ

On the Mach cone

u = 0, on n = 0 (7.159)

From the incompressible flow solution for a flow normal to a plate, one expects that u has a square-root singularity at the leading edge. Indeed, for a delta wing with

where C is a real constant (since the boundary conditions are homogeneous).

Obviously, C ^ 1 as m’ ^ 0 to recover the slender body solution for a delta wing with vanishing span.

The determination of C (to satisfy the boundary condition w = – a) is compli­cated. Referring to Ashley and Landhal [1]

(7.161)

where E (k) is the complete elliptic integral of second kind with modulus k. The pressure coefficient is given by

The lift coefficient is found to be

The above results are consistent with slender body theory for m = 1 (or k = 1) and with supersonic edge theory for m = 1 (or k = 0).

The drag is given by

for supersonic edges. When the leading edge is subsonic, Jones and Cohen [11] accounted for leading edge suction, where

D = L a – Fs

with their estimate of Fs