CONTROL-FREE NEUTRAL POINT

It is evident from the preceding comment that the N. P. of a tailed aircraft when the control is free is given by (6.3,36) as

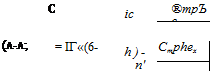Alternatively, we can derive the N. P. location from (6.6,56), for we know from (6.3,19) that

Since Gmg is of different form for the two main types of aircraft, we proceed separately below.

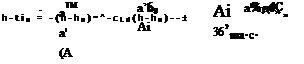Tailless Aircraft. Gmg is given by (6.4,9) and Chex = bv When these are substituted into (6.6,11) the result is

A, dde

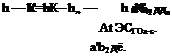By virtue of (6.6,6) this becomes

Tailed Aircraft. Cm is given by (6.4,8), so (6.6,11) becomes for this case

(h – Ъ’п) = – (Ь – K) – °^CLs(h – hnJ + aeVH a ab2 a’b2

Using (6.6,46) this becomes

h-h’n = h-~ iahn – h + ^faeVH

a’ b2 “7 a’62

We replace hnwb by (hnab – hn) + hn to get

Finally, using (6.4,8) for CL&, and (6.5,4) for Ghv we get

The difference (h! n — h) is called the control-free static margin, K’„. When representative numerical values are used in (6.6,13) one finds that hn — h’n may be typically about 0.08. This represents a substantial forward movement of the N. P., with consequent reduction of static margin, pitch stiffness, and stability.