Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
. ELEVATOR ANGLE TO TRIM
<7 = СЛос) + C, (5,
-”trim / і etrim
|
= CL(*)-<^Cm(*) ^m6 |
(6.4,11) |
|
When the linear lift and moment relations (6.4,2) apply the equations for trim are |
|
|
@Lxatrim + CiA. — CL •* trim trim ^maatrim ^md^eiTim ‘ |
(6.4,12) |
|
These equations are solved for a and de to give |
|
|
__ ___ @mpL$ + ®трІ4хіш ^trim д |
(a) |
|
s ^’mpLx ~b ^mpLtvim ^etrim д |
(6) (6.4,13) |
|
^^etrim ^Lxi}l h ) ^trim A ^ A ^ Я) |
(c) |
|
where A = CLCmg – СъСтл |
(d) |
|
and is normally negative. The values of A for the two types of airplane are readily calculated from (6.4,8 and 9) together with (6.3,19) to give |
|
|
Tailed: |
|
|
A = GL[CLg(hn ~ hnwb) — ae V h |
(a) |
|
Tailless: Д = Cr d°ma-c’ • a«5e |
(6.4,14) (6) V ‘ |
|
and both are independent of h. From (6.4,13») we get the trimmed lift curve: |
|
|
Gm 0Ts A fi ______ то Ьg – ° i«t rim p ‘ p atrim (-‘ms |
(6.4,16) |
|
and the slope is given by |
|
|
(d°L c Cl*c Uajlrim Gmg m° |
(6.4,16) |
|
|
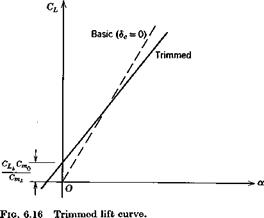
The trimmed lift-curve slope is seen to be less than CL by an amount that depends on (7 , i. e. on the static margin, and that vanishes when h hn.
The difference is only a few percent for tailed airplanes at normal C. G. position, but may be appreciable for tailless vehicles because of their larger CLa. The relation between the basic and trimmed lift curves is shown in Fig. 6.16.
Equation (6.4,136) is plotted on Fig. 6.17, showing how <5etrim varies with CT and C. G. position when the aerodynamic coefficients are constant.
■^trira
|
Fig. 6.17 Elevator angle to trim at various C. G. positions. |
