Integralgleichung fur die Zirkulationsverteilung nach der Tragflachentheorie

Um die Gleichung fiir die Berechnung der Zirkulationsverteilung aufzustellen, muB zunachst die Bedingung dafiir angegeben werden, daB die mit Wirbeln belegte tragende Flache eine Stromflache ist,
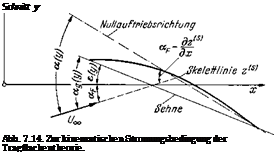
d. h., daB auf ihr die Normalkomponente der resultierenden Geschwindig – keit gleich Null ist. Dieses ist die sogenannte kinematische Stromungs – bedingung. In Abb. 7.14 ist ein Flugelschnitt у der tragenden Flache

I z

(Skelettflache) z^(x, y) dargestellt. Dieser wird mit der Geschwindig – keit Uoq angestromt, die mit der Sehne den geometrischen Anstell – winkel ocg(y) = <xF + e(y) bildet. Es ist <xF der Anstellwinkel, gemessen gegen die #-Achse, und e(y) der Verwindungswinkel. Bedeutet w(x, y) die in einem Punkt der x, y-Ebene vom gesamten Wirbelsystem in – duzierte Geschwindigkeit in z-Richtung (w > 0 in Richtung der posi – tiven z-Achse), dann lautet die kinematische Stromungsbedingung in Analogie zu Gl. (6.62):

(7.37)

Hierbei stellt die eckige Klammer den Winkel zwischen der Anstrom – richtung und der Skelett-Tangente dar. Es muB Gl. (7.37) in alien Punkten x, у der tragenden Flache erfiillt sein.

Weiterhin muB nun zunachst aus der vorgegebenen Wirbelverteilung k(x, y) die induzierte Geschwindigkeit w(x, y) auf der tragenden Flache ermittelt werden. Der Einfachheit halber berechnen wir jedoch die indu­zierte Geschwindigkeit in der Projektion der tragenden Flache auf die x, y-Ehene, die mit der Wirbelflache identisch ist. Die induzierte Ge­schwindigkeit w (x, у) in einem behebigen Punkt der x, y-Ebene wird erhalten, indem man zunachst den Beitrag eines Hufeisenwirbels eines Elementarflugels nach dem Biot-Savartschen Gesetz, Кар. 2.46, er­mittelt, Abb. 7.15. Die gesamte induzierte Geschwindigkeit w(x, y) ergibt sich daraus, daB man zuerst in der ^-Richtung uber einen Elementarfliigel und danach in der у-Richtung liber die Gesamtheit aller Elementarfliigel integriert. Die Ausfuhrung dieser Integrationen liefert,

wie in [73] im einzelnen dargestellt ist, folgendes:

mit

0(x, y y) = 2 J k(x’, y) dx’.

xv{y)

die induzierte Geschwindigkeit w(x, y) zu berechnen ist, zunachst auBerhalb der Wirbelflache annimmt (z =)= 0) und danach in die Wirbel­flache riicken laBt (z -> 0).[4] Fiihrt man schlieBlich Gl. (7.38) in die kinematische Stromungs – bedingung (7.37) ein, so erhalt man:

Bei der Herleitung der Gin. (7.38) und (7.39) ist das Biot-Savartsche Gesetz in der Weise anzuwenden, daft man den Aufpunkt, in welchem

Dabei hangt в(х, у; у’) nach Gl. (7.39) mit k(x, y) zusammen. Gl. (7.40) ist bei vorgegebenem Anstellwinkel ocF und vorgegebener Form der Tragflache (x, y) eine Integralgleichung fur die Zirkulationsver-

teilung k(x, y) der tragenden Flache (zweite Hauptaufgabe). Damit fur die Tragflache die Kuttasche AbfluBbedingung erfiillt ist, muB die Wirbeldichte к (x, y) an der Hinterkante x = xh (y) verschwinden, vgl. Gl. (6.64). Nachdem aus Gl. (7.40) die Wirbeldichte k(x, y) ermittelt worden ist, erhalt man die resultierende Druckverteilung von Unter – und

Oberseite in einem Punkt x, у nach Gl. (6.65) in der Form:

= (7.41)

Я. оо U oo

Hierin ist qoo = q t/^/2 der Staudruck der Anstromung. Der ortliche Auftriebsbeiwert ca(y) eines Fliigelschnittes у ergibt sich durch Inte­gration der Druckverteilung liber die Fliigeltiefe analog zu Gl. (6.66):

Xh(y)

ca(y) = Лср(х, у) dx. (7.42)

xv{y)

Den Gesamtauftriebsbeiwert cA = A/Fq^ des Fliigels erhalt man schlieBlich zu

s

cA = jJJ Acpdxdy = j J ca(y) l(y) dy. (7.43)

(F) – t

Man vergleiche hierzu Gl. (5.42).

Wie bei der Prandtlschen Traglinientheorie (Кар. 7.13) lafit sich bei vorgegebener Fliigelflache und vorgegebener Wirbelverteilung k(x, y) die Fliigelgeometrie (Verwindung und Wolbung) nach Gl. (7.40) ermit – teln. Diese Entwurfsaufgabe (erste Hauptaufgabe) erfordert Quadra – turen nach GL (7.39) und (7.40). Einige Beispiele hierzu wurden erst – malig von H. Blenk [4] angegeben.

Bei vorgegebener Fliigelgeometrie (GrundriB und Anstellwinkel) liefert Gl. (7.40) die Wirbelverteilung uber die Fliigelflache. Diese Nach – rechnungsaufgabe (zweite Hauptaufgabe) fiihrt auf eine Integralgleichung fur die Wirbelverteilung k(x, y), welche erhebliche mathematische Schwie – rigkeiten bereitet. Man ist deshalb fur die Losung dieser Integralgleichung auf Naherungsverfahren angewiesen, die in verschiedener Weise an – gesetzt werden konnen.

Eine erste Moglichkeit, Naherungslosungen zu gewinnen, besteht darin, daB man die Form der Wirbelverteilung k(x, y) in Spannweiten – richtung у vorgibt. Wahlt man fur k(y) einen Ansatz mit m Gliedern, von denen das erste z. B. die elliptische Verteilung darstellt, so kann die Integralgleichung (7.40) nicht mehr auf der ganzen tragenden Flache, sondern nur noch in m Schnitten in Richtung der Fliigeltiefe erfiillt werden.

Eine zweite Moglichkeit zur Beschaffung von Naherungslosungen besteht darin, die Form der Wirbelverteilung k(x, y) in Richtung der Fliigeltiefe x vorzugeben, z. B. durch die Birnbaumschen Normalvertei – lungen nach Gl. (6.71). Wahlt man fur k(x) einen Ansatz mit n Gliedern, so kann die Integralgleichung nur auf n Linien langs der Spannweite
erfullt werden. Solche Verfahren wurden fiir n — 1 (1. Birnbaumsche Verteilung) von J. Weissinger [83] und fiir n — 2 (1. und 2. Birn­baumsche Verteilung) von H. Multhopp [58] und E. Truckenbrodt [75] sowie fiir n = 5 von S. Wagner [80] ausgearbeitet.

Eine dritte Moglichkeit besteht darin, dab man gleichzeitig Vertei – lungen iiber die Spannweite mit m Gliedern und Verteilungen iiber die Tiefe mit n Gliedern vorgibt. In diesem Fall kann man die Integral – gleichung in m • n Punkten erfiillen, die in Spannweiten – und Tiefen – richtung geeignet zu verteilen sind. Ein solches Verfahren hat schon friihzeitig H. Blenk [4] angewendet.