Laminar Boundary Layer Theory (Prandtl 1904)

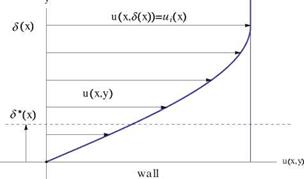
Let S be the boundary layer thickness which represents the limit beyond which viscous effects are negligible. Let l be the characteristic length of the obstacle. We assume that S ^ l, see Fig. 8.6. Inside the boundary layer one can simplify the Navier-Stokes equations, using order of magnitude analysis which is based on the rigorous technique of asymptotic expansion. The м-component of velocity is of order U, the incoming flow velocity. Pressure is assumed to be of order p = O (pU2), in other words, it can be written

Fig. 8.6 Geometric interpretation of displacement thickness S* (x)

P(x, y) = pu2n(<8 27)

where П is a dimensionless function of x/1 and y/6(x) only. The coefficient in front of the dimensionless function, pU2, is called a “gage”. It gives the order of magnitude of the term. Furthermore, the partial derivatives are of order, respectively:

	d2 d2 dx2 « dy2
(8.28)

(a) From continuity, the two terms must balance, hence

(8.29)

The flow is almost aligned with the body.

(b) From the x-momentum equation: the acceleration terms in the left-hand-side are both of order O (pu^j and must balance the viscous term р,^ = о (pjU^j, hence

(8.30)

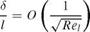
where the Reynolds number is defined as Rel = pU. In fact, this is true for any x sufficiently large, i. e.

where Rex = pUx. Note that if there is a pressure gradient in the x-direction, its order will match the other terms, as dp = о (p ufsj.

(c) Consider the y-momentum equation. First we multiply it by |: the acceleration terms in the left-hand-side are both now of order O (pир^ and balance the viscous

term of order O (p U^ as a consequence of the previous result (indeed, one term и has been replaced by v in both sides). The pressure derivative term is now of order O (pир. Comparing this term’s magnitude with the other terms indicates that this term dominates the equation since

U2	U262	U2	( 62
l > p 13	= pT	U) *
d p	dv	dv	d2v
dy y> pu dx	+pv d	0Г Pdy-2

As a result, to first order, the y-momentum equation reduces to one term and the pressure gradient in the y-direction must vanish

^ = 0 ^ p = p(x) = pi (x) (8.33)

d y

where the subscript i stands for “inviscid”, i. e. in the inviscid flow. Let ui (x) be the inviscid flow velocity at the edge of the boundary layer. From Bernoulli’s equation

p™ + [7] pU2 = pi (x) + 2p (u2(x) + v2(x)) ~ pi (x) + 2pu2(x) (8.34)

Taking the derivative in the x-direction yields

d2 u

Hence the Prandtl boundary layer equations reduce to

This is a nonlinear system of two equations in two unknowns, (u, v) with a source term function of ui (x) provided by the inviscid flow. It is of parabolic type and can be marched in the flow direction as long as u(x, y) > 0.

The initial/boundary conditions are the following:

• at x = 0 u(0, y) = U, v(0, y) = 0, a uniform, undisturbed velocity profile is given,

• at y = 0, u(x, 0) = v(x, 0) = 0, along the solid wall,

• at y = S(x), u (x, S(x)) = ui (x), at the edge of the boundary layer.