LINEAR LIFT AND MOMENT

When the forces and moments on the wing, body, tail, and propulsive system are linear in a, as may be near enough the case in reality, some

additional useful relations can be obtained. We then have

Furthermore, if Ст<л is linear in CL, it follows from (6.3,4) that Gm does not vary with CL, i. e. that a true aerodynamic center exists. Figure 6.10 shows that the tail angle of attack is

at — awb + *’* — e

and hence

@Lt = aAamb + h ~ e)

The downwash є can usually be adequately approximated by

■ де

e = €0 — a,

9a

The downwash eg at CL = 0 results from the induced velocity field of the body and from wing twist; the latter produces a vortex wake and downwash field even at zero total lift. The constant derivative 9e/9a occurs because the main contribution to the downwash at the tail comes from the wing trailing vortex wake, the strength of which is, in the linear case, proportional to CL.

The tail lift coefficient then is

and the total lift, from (6.3,14) is CL = – л jx * wo^wb i—– 1 i—‘ + s5 а і 9a/J , St + at ~z (*< О “ €o) (a) or Cl = (CL)o + aV-wb (b) (6.3,29) or Cl = act. at ~ (h (e) where II e o’ “ eo) (6.3,30) is the lift of the tail when a. wb = 0;

(■-!)] (взл1>

is the lift-curve slope of the whole configuration; and a is the angle of attack

Fig. 6.12 Graph of total lift.

of the zero-lift line of the whole configuration (see Fig. 6.12). Note that, since it is negative, then (CL)0 is negative. The difference between a and awb is found by equating (6.3,296 and c) to be

at,

* – «-wb = – ~ (h ~ eo)
a 8

When the linear relations for CL, CLi and Gm^

Note that since Cm is the pitching moment at zero a. wb, not at zero total lift, its value depends on h (via VH), whereas Cm, being the moment at zero total lift, represents a couple and is hence independent of C. G. position. All the above relations apply to tailless aircraft by putting VH = 0. Another useful relation comes from integrating (6.3,19), i. e.

Cm = + Gift1 ~ K)

or Cm = Ст0 + – h„)

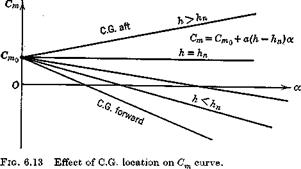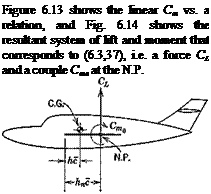
Fig. 6.14 Total lift and moment act­ing on vehicle.