LONGITUDINAL CONTROL

In this section we discuss the longitudinal control of the vehicle from a static point of view. That is, we concern ourselves with how the equilibrium state of steady rectilinear flight is governed by the available controls. Basically there are two kinds of changes that can be made by the pilot or
automatic control system—a change of propulsive thrust, or a change of configuration. Included in the latter are the operation of aerodynamic controls—elevators, wing flaps, spoilers, and horizontal tail rotation. Since the equilibrium state is dominated by the requirement Cm — 0, the most powerful controls are those that have the greatest effect on Cm.

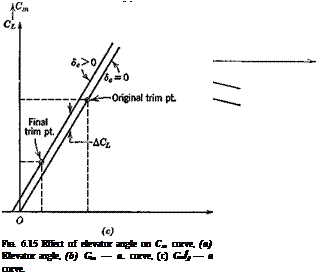
Figure 6.13 shows that another theoretically possible way of changing the trim condition is to move the C. G., which changes the value of a at which Cm = 0. Moving it forward reduces the trim a or CL, and hence produces an increase in the trim speed. This method was actually used by Lilienthal, a pioneer of aviation, in gliding flights during 1891—1896, in which he shifted his body to move the C. G. It has the inherent disadvantage, apart from practical difficulties, of changing Gmat the same time, reducing the pitch stiffness and hence stability, when the trim speed is reduced.

The longitudinal control now generally used is aerodynamic. A variable pitching moment is provided by moving the elevator, which may be all or part of the tail, or a trailing-edge flap in a tailless design. Deflection of the elevator through an angle ёе produces increments in both the Gm and CL of the airplane. The ДCL caused by the elevator of aircraft with tails is small enough to be neglected for many purposes. This is not so for tailless aircraft, where the ACL due to elevators is usually significant. We shall assume that the lift and moment increments for both kinds of airplane are linear in de, which is a fair representation of the characteristics of typical controls at high Reynolds number. Therefore,

Cl — Clxx + C, LSde Cm = + Стаде

THE DERIVATIVES CLg AND Cm6

Equation (6.3,14) gives the vehicle lift, with St = 0 for tailless types, of course. Hence

in which only the first term applies for tailless aircraft and the second for conventional tail elevators or all moving tails (when it is used instead of de).

We define the elevator lift effectiveness as

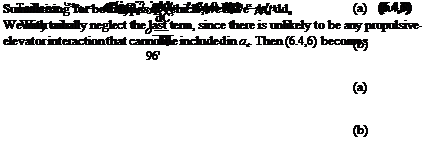The total vehicle Cm is given for both tailed and tailless types by (6.3,15). For the latter, of course, VB = 0. Taking the derivative w. r.t. de gives

In the last case, the subscript wb is, of course, redundant and has been dropped. The primary parameters to be predicted or measured are ae for tailed aircraft, and dCLjdde, дСт /дде for tailless.

a«C’