MODELS FOR NOISE/ERROR PROCESSES

The usual assumption is that noise is a white and Gaussian process. White noise has theoretically infinite bandwidth and it is an unpredictable process and hence has no model structure. It is described by a mean value and spectral density/covariance matrix. The noise affecting the system can often be considered as unknown but with bounded amplitude/uncertainty. One should search the models that are consistent with this description of the noise/error processes [13].

1.3.1 Continuous-Time/Discrete-Time White/Correlated

Noise Processes

We consider the continuous-time white noise process with the spectral density (S2) passing through a sampling process to obtain the discrete-time white noise process as shown in Figure 2.12. The output is a sequence with variance Q (a different numerical value) and is a discrete process. If the sampling time/interval is increased then, more and more of the power at more and higher frequencies of the input white process will be attenuated and the filtered process will have a finite power.

Variance — S2/sampling interval (At)

We see that as the sampling time tends to zero, the white noise sequence tends to be a continuous one and the variance tends to infinity. In reality such a process does not exist. Hence, the noise is fictitious. In practice the statistical characteristic of (continuous-time) white noise is described in terms of its spectral density, i. e., power per unit bandwidth.

If we pass uncorrelated noise signal (w) through a linear first-order feedback system, a correlated noise signal (v) is generated:

v — —fiv + w

Such correlated signal/noise process would arise in practice if the process is affected by some dynamic system, e. g., turbulence on aircraft (Appendix A) [14].

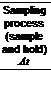
White noise with
spectral density
S-continuous process

Assume that a signal has a component that drifts slowly with a constant rate equal to b. Then the model is given as

X 1 = X2

x 2 = 0

Assume that x2 = b. The signal x1 is also called the random ramp process. In a sensor fault detection application [15], one can use the innovation sequence to detect the drift in the system/signal using this model. The point is that when a system/sensor is gradually deteriorating, in a sensor fault detection/identification/isolation scheme, and if the trend (drift) in the innovation (i. e., estimation residuals, Chapter 9) can be tracked by using the drift model, then the direction of occurrence or onset of the fault can be observed.