Number of Blades

The selection of the number of blades for a rotor (for a given blade area or solidity) is usually based on dynamic rather than aerodynamic criteria, that is, it is based on the mini­mization of vibratory loads, which is easier for rotors that use a larger number of blades. Fewer blades, however, will usually reduce blade and hub weight, minimize hub drag, and may give better reliability and maintainability because of a lower parts count. Lighter weight helicopters usually have two blades, whereas heavier helicopters generally have four, five, seven or even eight blades. As shown in Section 3.2.4, aerodynamically the induced tip-loss effects are reduced by increasing the number of blades, but the effects on induced power are relatively small for the high aspect ratio blades typical of helicopter rotors.

Knight & Hefner (1937) and Landgrebe (1972) have conducted systematic tests of blade number and solidity on rotor performance. Knight & Hefner tested subscale rotors with two, three, four, and five blades with no twist and at fairly low tip speeds. Landgrebe tested subscale rotors with two, four, six, and eight blades, linear twist, and at full-scale tip Mach numbers. All of the tests were done by adding blades to the rotor hub so the results cannot distinguish independently the effects of solidity from the number of blades. However, an analysis of these data suggest that hover performance is primarily affected by rotor solidity; the number of blades are secondary. Following Knight & Hefner (1937), the primary rotor behavior can be analyzed by the use of the blade element theory. From Section 3.2, the rotor-thrust coefficient is given by

(6.6)

Also, ф{г) = X/r, and for a linearly twisted blade 0(r) = #75 + #tw(r — 0.75). Therefore

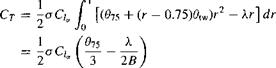(6.7)

when including tip losses alone through the factor B. Assuming uniform inflow, the corre­sponding power can be written as

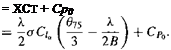(6.8)

Incorporating other nonideal induced losses (other than tip loss) such that X = Ky/Cp/2 and dividing through by a3 gives

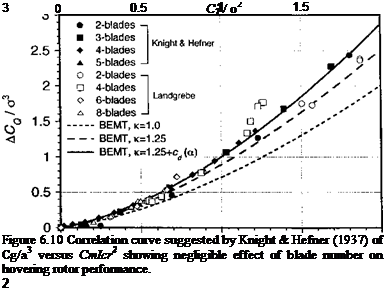Therefore, if the results from rotor experiments are plotted in the form of (Cp — Cp0)/a3 versus Ст/cr2, then this should remove the primary effect of solidity from the measure­ments. As shown by Figure 6.10, the results from both sets of measurements show good correlation with the result given by Eq. 6.9, confirming that the effect of blade number on rotor performance is indeed secondary. The modified results are based on the assumption that к — 1.25, В — 0.97 and a higher-order approximation for the profile power, both effects having been discussed previously in Section 3.3.9. Note that the latter assumption gives a small but significant improvement in the correlation at high values of thrust where

nonlinear drag effects begin to become important as the boundary layer thickens and the blade sections approach stall.

In subscale rotor experiments the effects of blade number can be masked by other effects, including those associated with the effects of Reynolds number and Mach number. The effects of Reynolds number can be particularly significant on small-scale rotors with small chords and tip Reynolds numbers that are often below 106 – see Section 7.9.1. Increasing the number of blades while maintaining the solidity of the rotor will decrease the blade chord and decrease the Reynolds numbers. Based on 2-D arguments this will tend to result in slightly higher values of the profile drag coefficient and, therefore, will give a small but finite reduction in the figure of merit.

A larger number of blades also leads to weaker tip vortices (for the same overall rotor thmst), thus potentially reducing the intensity of any airloads produced by blade-vortex interactions (all other factors being assumed equal). However, with more blades, the number of potential blade-vortex interactions over the disk will be increased (see Section 10.4.2). This can affect both the frequency and directivity of propagated noise, and the problem becomes far too complicated to make generalizations as to the expected trends. Furthermore, from the perspective of noise generation, a higher number of blades results in a smaller chord and lower “thickness” noise associated with each blade. However, even though the strengths of the tip vortices may be reduced by using a larger number of blades (at a constant thrust), the blades are closer azimuthally. Because the tip vortices are convected vertically only relatively slowly in hover and remain almost in the plane of the rotor, the following blades may more closely interact with the vortices from previous blades. Such a phenomenon has been encountered on hovering rotors with five or seven blades and can significantly affect predictions of induced power – see Clark & Leiper (1970).