Rectangular Wings at Angle of Attack

Assuming small disturbances, the flow past a rectangular wing is two-dimensional except within the mach cones generated at the tips, where conical flow exists, Fig. 7.26.

For the region outside the Mach cone, a transformation similar to Chaplygin’s produces two-dimensional wave equation. The solutions in the hyperbolic and elliptic regions must be joined such that the velocity components are continuous across the Mach cone.

More complicated analysis includes, Prandtl-Meyer’s expansion, shock waves and formation of vortex flow.

7.9.2 Numerical Solution of Conical Euler Equations

The conservation laws in conical coordinates are given by (see Powell [33, 34]) r d U r д д d

КИТ + К2 dr (F + nG + ZH) + ^ (G – nF) + — (H – ZF) + 2F = 0

(7.167)

where

r = x2 + y2 + z2, n = , Z = , К = 1 + n2 + Z2

U, F, G and H are the standard state vector and flux vectors of the Euler equations in Cartesian coordinates.

The conical velocities are given by

uK = u + nv + Zw (7.169)

un = v — nu (7.170)

u z = w — Z u (7.171)

For conical flows, dU/dr = 0 and the boundary conditions must be consistent with conical flow assumption.

The governing equations become

к d	1 1 Ъ ____ 1	d	pun puun — np	d	p u Z puuz — ZP		pu pu2 + p
Г d t	pv	+ dn	p uun + p	+ dZ	pvuZ	+ 2	puv
pw	pwun	pwuZ+p		puw
	p E		p Hun		p Huz		puH

(7.172)

where H = E + р/р.

Based on topological considerations, Powell indicated that the physically mean­ingful singularities of conical flows are nodes, saddles and spirals.

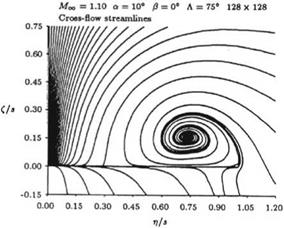A cell vertex, finite volume, multi-stage Runge-Kutta scheme, with added artificial viscosity, was used to obtain numerical solutions over delta wings with grid gener­ation allowing multiple levels of refinement. Typical results are shown in Fig.7.27 (from Ref. [33, 34]).

The above study concluded that low pressure and density were seen in the vortex region.

Numerical parameters such as grid resolution and artificial viscosity did not affect the level of the total pressure loss, only the distribution of it. Modeling the core region remains however to be a problem.

In general, the conical flow calculation is less expensive than the full three­dimensional one. However, since the conical flow is supersonic everywhere, a space marching technique is an alternative. simply, artificial time is equivalent to a certain space marching and the latter is less restrictive.

Today, full three-dimensional Navier-Stokes solutions for high speed flows over delta wings are available, including simulation of important phenomena, for example vortex breakdown. CFD was an important tool in modifying the design of fighter jets where the vortex generated from the leading edge and its interaction with the tail was a serious problem.