Rotor Diameter

There are several conflicting factors that must be examined when determining the main rotor diameter. As shown previously in Chapters 2 and 5, both good hover performance and safe autorotational capabilities call for a large rotor diameter. The advantages of a larger rotor diameter are lower disk loadings, lower average induced velocities, and lower induced power requirements. It was shown in Section 2.12 that based on the modified momentum theory the operating thrust coefficient, Cj, to give the best power loading was

(6.1)

which depends on airfoil section, rotor solidity and induced power factor. Using this result, the disk loading for minimum power loading will be

This equation determines the optimum radius of the rotor to maximize power loading at a given gross weight. Solving for the main rotor radius gives

imed that for design purposes each rotor of the dual rotor helicopter carries one half of the total weight of the aircraft. It has also been shown that

T FM

PL = — oc—— ,

P DL

which means for a given disk loading the rotor(s) should also be operated at the highest possible figure of merit. However, Fig. 2.16 has shown that the most efficient power loading (compared to the ideal value) is relatively insensitive to the operating state of the rotor, in that the power loading curve is fairly flat over the normal range of operational thrust coeffi­cients. Therefore, there is some latitude in selecting rotor radius, which may be constrained
because of factors other than pure aerodynamic considerations. For example, if the heli­copter is required to operate off loose terrain such as gravel or sand, the design may require the disk loading to be limited so that the downwash velocities remain low enough not to stir up any of the loose surface material. This usually means the use of a relatively high rotor diameter. A large diameter also means a larger inertia and stored rotational kinetic energy, which is essential for safe autorotational characteristics (see Section 5.6). Initial sizing studies of the main rotor must always consider autorotational capability, which will require some minimum rotor inertia if the helicopter is to meet the military acceptance criteria or civilian certification requirements. Both single and multiengine helicopters must demonstrate safe autorotative landing capability at maximum gross weights. Often the ini­tial rotor design is guided by previous rotor designs that are known to meet the autorotative specifications necessary for certification. An autorotative index of the form that was dis­cussed in Section 5.6.3 may be used as a means of quantifying the potential autorotative characteristics of a proposed new rotor design.

Usually a much smaller rotor diameter must ultimately be used than would be desired for best hovering efficiency (for a given blade area and tip speed) so as to meet overall helicopter size, weight, cost, gearbox torque limitations, speed, maneuverability requirements, and storage or transportation requirements for the helicopter. A smaller rotor will have a smaller and lighter hub and a lower overall parasitic drag, and so this will be more efficient for cruising flight. Smaller rotors also permit a more compact net helicopter design, which is useful for several operational reasons, including storage and transportation by sea and air. In addition, a smaller rotor diameter minimizes the static deflection or “droop” of the nonrotating blades. The static droop can increase quickly for larger rotor diameters and may cause problems when starting and stopping the rotor, especially in gusty wind conditions where the low centrifugal forces on the blades may lead to “blade sailing,” causing the rotor blades to flap and flex and perhaps impact the airframe. In most cases, the blade radius is usually kept to less than about 40 ft (12 m) otherwise the extra structure necessary to increase the blade stiffness will incur a significant weight penalty.

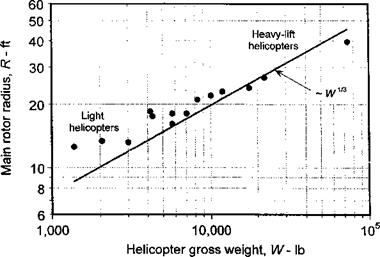
Figure 6.3 gives a summary of main rotor radius versus gross weight for a selection of helicopters (see appendix). Plotting the data on a logarithmic scale accentuates the

strong correlation between the quantities. This plot shows that the helicopter weight grows much faster than the rotor size. The well-known “square-cube” scaling law gives a simple explanation for this behavior. For geometrically similar aircraft, the overall area of the aircraft increases with the square of a characteristic length, say /, and its volume by the cube of this length; so the weight of the aircraft, W, should also increase with the cube power of a characteristic length, that is, W а Iі or l oc W1/3. Therefore, for a helicopter R oc VF1/3, which indeed is the trend shown in Fig. 6.3.

The corresponding trend of rotor disk loading versus gross weight is shown in Fig. 6.4. Remember that the disk loading must be kept as low as possible to maximize hovering performance, although with the larger and heavier helicopters this comes at some price. Because of the various other nonaerodynamic constraints posed in the design, such as the minimization of rotor weight and greater torque requirements, a large rotor diameter is not always practical. Generally, the manufacturer will try to find the smallest rotor diameter that will meet all of the specifications laid down for that helicopter. The square-cube law would suggest that T/A ос 1У1/3, but the results shown in Fig. 6.4 indicate a slightly more rapid increase such that T/A oc W2/5 because of the nonaerodynamic constraints. Therefore, the corresponding power loading will be proportional to W-1/5.