Solution

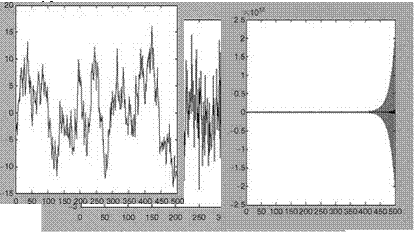Generate Gaussian random noise sequence by u = randn(500,1). Then standardize the sequence by un = (u — mean(u))/std(u). The sequence u has mean = —0.0629 and std = 0.9467. The sequence un has mean = —1.8958e — 017 and std = 1. The noise sequence un is plotted in Figure 2.11a. The sequence y(k) is generated using the following steps: y(1) = 0.0 + 2* un(1); y(2) = 0.0 + un(2); for k = 3:500; y(k) = 0.9* y(k— 1) + 0.05*y(k—2) + 2* un(k); end; plot(un); plot(y) (see Figure 2.11b). The SNR = 20 log 10(var(y)/var(un)) = 31.1754. We see that the model is a stable one and hence generates a stable time series, because roots ([1 —0.9 —0.05]) are 0.9525 and —0.0525 and both are within unit circle in the z-domain/complex plane. If any one root

(b) (c)

FIGURE 2.11 (a) The noise sequence ‘‘un’’ with zero mean and std = 1.0; (b) the stable time

series y; (c) the unstable time series y.

is greater than 1, then the time series will be unstable. Generate the unstable time series by y(k) — —1.01 * y(k—1) + 0.05 * y(k—2) + 2 * un(k) (Figure 2.11c). We see that the new model is unstable and hence generates unstable time series, since roots ([1 1.01—0.05]) are —1.0573 and 0.0473 and one root is out of the unit circle in the z-complex plane.