Spatial Discretization in Wave Number Space

In this chapter, how to form finite difference approximations to partial derivatives of the spatial coordinates is considered. The standard approach assumes that the mesh size goes to zero, i. e., Ax ^ 0, in formulating finite difference approximations. However, in real applications, Ax is never equal to zero. It is, therefore, useful to realize that it is possible to develop an accurate approximation to d/dx by a finite difference quotient with finite Ax. Many finite difference approximations are based on truncated Taylor series expansions. Here, a very different approach is introduced. It will be shown that finite difference approximation may be formulated in wavenumber space. There are advantages in using a wave number approach. They will be elaborated throughout this book.

2.1 Truncated Taylor Series Method

A standard way to form finite difference approximations to d/dx is to use Taylor series truncation. Let the x-axis be divided into a regular grid with spacing Ax. Index I (integer) will be used to denote the 1th grid point. On applying Taylor series expansion as Ax ^ 0, it is easy to find (xt = I Ax) as follows:

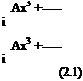9 u 1 d2u 2 1

“’+■ = u(x’ + Ax) = u‘ + jїї),Ax + 2 j a?) Ax + 3!

j du) 1 j d 2u) 2 1

"’-■ = u(xt – Ax) = ,,t – – tAx + 2 ^ – j!

Thus,

„ j 9 u ) 1 j 9 3u ) 3

“<+1-u’-1 = 2Ax Vx, + 3 ,Ax +

On neglecting higher-order terms, a second-order central difference approximation is obtained,

(2.2)

This is a 3-point second-order stencil. By keeping a larger number of terms in (2.1) before truncation, it is easy to derive the following 5-point fourth-order stencil and the 7-point sixth-order stencil as follows:

From the order of the truncation error, one expects that the 7-point stencil is probably a more accurate approximation than the 5-point stencil, which is, in turn, more accurate than the 3-point stencil. However, how much better, and in what sense it is better, are not clear. These are the glaring weaknesses of the Taylor series truncation method.

2.2 Optimized Finite Difference Approximation in Wave Number Space

Suppose a central (2N + 1)-point stencil is used to approximate 9/9x; i. e.,

At one’s disposal are the stencil coefficients a; j = – N to N. These coefficients will now be chosen such that the Fourier transform of the right side of Eq. (2.5) is a good approximation of that of the left side, for arbitrary function f. Fourier transform is defined only for functions of a continuous variable. For this purpose, Eq. (2.5), which relates the values of a set of points spaced Ax apart, is assumed to hold for any similar set of points Ax apart along the x-axis. The generalized form of Eq. (2.5), applicable to the continuous variable x, is

Eq. (2.5) is a special case of Eq. (2.6). By setting x = lAx in Eq. (2.6), Eq. (2.5) is recovered.

The Fourier transform of a function F(x) and its inverse are related by

(Ю

F (a) = E [ f (x)e-iaxdx 2n J

— TO TO

F (x) =/ F (27)

— TO

The following useful theorems concerning Fourier transform are proven in Appendix A.

2.2.1 Derivative Theorem

Transform of 8

d x