Supersonic Area Rule

Hayes [27] derived a formula for the wave drag of a wing-body configuration of arbitrary thickness distribution and experiencing both lift and side forces.

For a thin non lifting wing, the source distribution is related to the geometry via (see Ashley and Landhal [1])

q(x, y) = _дд (7.123)

д x

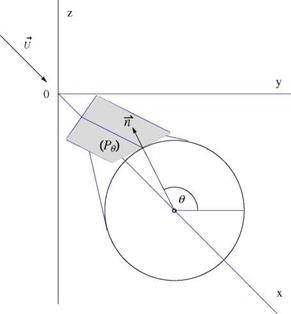
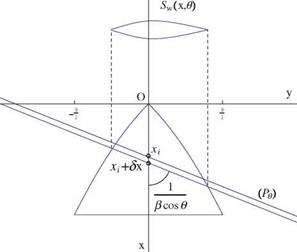
Consider the Mach planes passing through a point xi along the x-axis and tangent to the Mach cone with apex at xi, see Fig. 7.18. Let в be the angle of the normal to the plane with the y-axis. The equation of such a plane is (Pe ) : x — xi + вy cos в + вz sin в. The intersection of two parallel neighboring Mach planes with the (x, y)- plane is shown in Fig. 7.19. The intersection with the slender wing is projected on a plane normal to the axis as Sw(x, в), also shown in the figure. Then upon integrating in y and lumping the source along the x-axis, on finds

nr m f дg(xi + вy cos в, y)

Q(xi, в) = _ — dy

д д x

Sw (x, в)

(7.124)

_ g(xi + вy cos в, y)dy

Fig. 7.18 Mach cone and Mach plane

Fig. 7.19 Section of wing by characteristic plane (Pg)

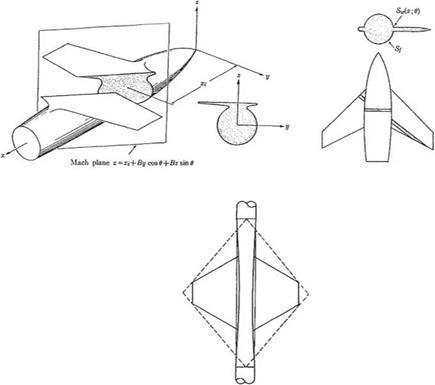
Fig. 7.20 Supersonic area rule methodology (from Aerodynamics of Wings and Body, by H. Ashley and M. Landhal, with kind permission of Dover Publication, 1985 edition)

For a body of revolution

Q(Xi) ~ Sf (xi) (7.125)

since, for a slender body, the area of the oblique cut will not differ much from its projection.

For a winged body of revolution, the area distribution of the equivalent body is

S(x,0) = Sf (x) + Sw(x ,0) (7.126)

Following Lomax and Heaslet [28], Fig. 7.20, the effect of wing-body interference can be represented through

Se (x) = Sf (x) + A0(x) (7.127)

where

1 r2n,

A0(x) = Sw(x, 0)d0 (7.128)

2n 0

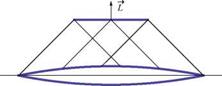
Fig. 7.21 Flat plate lift induced by a body of revolution in supersonic flow

Minimum wave drag (for non lifting configuration) can be achieved by choosing Se (x) to be an optimum shape, i. e. the Sears-Haaks body. Thus the fuselage will be indented in the region of the wing.

If the body is approximated by an infinite cylinder, the optimum body indentation is then given by

A Sf + Ao(x) = 0 (7.129)

The above supersonic area rule includes the transonic area rule, in the limit of M0 ^ 1.

Jones [11, 12], considered the lifting case, including the vortex drag and concluded that the total drag would be minimized for elliptic loading. The three-dimensional drag for a straight elliptic wing will be always greater than the two-dimensional drag.

Lower values, however, can be obtained by yawing the wing behind the Mach cone.

The wave drag interference between lift and thickness is zero for a mid wing body. A favorable interaction is possible (see Ferri et al. [29]).

For a flat plate at zero angle of attack located above the body, a lift will be generated without drag, and the drag of the body will be lower due to the wave reflection from the wing impinging on the rear part of the body (Ashley andLandhal [1]), Fig.7.21.