The development of aerofoil theory

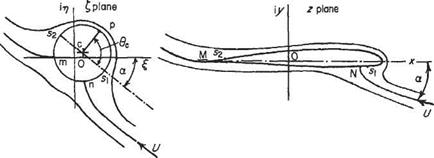
The first successful aerofoil theory was developed by Zhukovsky.* This was based on a very elegant mathematical concept – the conformal transformation – that exploits the theory of complex variables. Any two-dimensional potential flow can be repre­sented by an analytical function of a complex variable. The basic idea behind Zhukovsky’s theory is to take a circle in the complex £ = (£ + і7;) plane (noting that here C does not denote vorticity) and map (or transform) it into an aerofoil-shaped contour. This is illustrated in Fig. 4.8.

A potential flow can be represented by a complex potential defined by Ф = ф + it’ where, as previously, ф and </> are the velocity potential and stream function respect­ively. The same Zhukovsky mapping (or transformation), expressed mathematically as

C2

(where C is a parameter), would then map the complex potential flow around the circle in the f-plane to the corresponding flow around the aerofoil in the z-plane. This makes it possible to use the results for the cylinder with circulation (see Section 3.3.10) to calculate the flow around an aerofoil. The magnitude of the circulation is chosen so as to satisfy the Kutta condition in the r-plane.

From a practical point of view Zhukovsky’s theory suffered an important draw­back. It only applied to a particular family of aerofoil shapes. Moreover, all the

members of this family of shapes have a cusped trailing edge whereas the aerofoils used in practical aerodynamics have trailing edges with finite angles. Karman and Trefftz[13] later devised a more general conformal transformation that gave a family of aerofoils with trailing edges of finite angle. Aerofoil theory based on conformal transformation became a practical tool for aerodynamic design in 1931 when the American engineer TheodorsenT developed a method for aerofoils of arbitrary shape. The method has continued to be developed well into the second half of the twentieth century. Advanced versions of the method exploited modern computing techniques like the Fast Fourier Transform.[14]

If aerodynamic design were to involve only two-dimensional flows at low speeds, design methods based on conformal transformation would be a good choice. How­ever, the technique cannot be extended to three-dimensional or high-speed flows. For this reason it is no longer widely used in aerodynamic design. Methods based on conformal transformation are not discussed further here. Instead two approaches, namely thin aerofoil theory and computational boundary element (or panel) methods, which can be extended to three-dimensional flows will be described.

The Zhukovsky theory was of little or no direct use in practical aerofoil design. Nevertheless it introduced some features that are basic to any aerofoil theory. Firstly, the overall lift is proportional to the circulation generated, and secondly, the magni­tude of the circulation must be such as to keep the velocity finite at the trailing edge, in accordance with the Kutta condition.

It is not necessary to suppose the vorticity that gives rise to the circulation be due to a single vortex. Instead the vorticity can be distributed throughout the region enclosed by the aerofoil profile or even on the aerofoil surface. But the magnitude of circulation generated by all this vorticity must still be such as to satisfy the Kutta condition. A simple version of this concept is to concentrate the vortex distribution on the camber line as suggested by Fig. 4.9. In this form, it becomes the basis of the classic thin aerofoil theory developed by Munk* and Glauert.8

Glauert’s version of the theory was based on a sort of reverse Zhukovsky trans­formation that exploited the not unreasonable assumption that practical aerofoils are

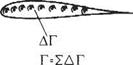
Fig. 4.9 thin. He was thereby able to determine the aerofoil shape required for specified aerofoil characteristics. This made the theory a practical tool for aerodynamic design. However, as remarked above, the use of conformal transformation is restricted to two dimensions. Fortunately, it is not necessary to use Glauerl’s approach to obtain his final results. In Section 4.3, later developments are followed using a method that does not depend on conformal transformation in any way and. accordingly, in principle at least, can be extended to three dimensions.

Thin aerofoil theory and its applications are described in Sections 4.3 to 4.9. As the name suggests the method is restricted to thin aerofoils with small camber at small angles of attack. This is not a major drawback since most practical wings are fairly thin. A modern computational method that is not restricted to thin aerofoils is described in Section 4.10. This is based on the extension of the panel method of Section 3.5 to lifting flows. It was developed in the late 1950s and early 1960s by Hess and Smith at Douglas Aircraft Company.