THE EFFECT OF ELASTIC DEFORMATION ON THE STATIC LONGITUDINAL STABILITY OF AN AIRPLANE
The static longitudinal stability is measured by the derivative dCM/dCL at the symmetrical level flight condition, where CL is the total lift coefficient and CM is the coefficient of the pitching moment about the airplane center of gravity. An airplane is statically stable when 5CMjc>CL is negative. In power-off condition and for the rearmost center of gravity location, a value of — ЪСм/дСь from 0.10 to 0.15 usually leads to satisfactory results. A study of the pitching moment about the center of
gravity in steady flight is a very complex one when the effects of power, component interference, and free controls are taken into account. However, a large amount of experimental data has been gathered in the past, and the determination of the dCMjdCL derivative for a rigid airplane offers no serious difficulty, even in the most complicated cases.[12]
If the airplane is not rigid, the static longitudinal stability derivative will be affected by the elastic bending of the fuselage and the twisting of the wing and tail surfaces. Let us consider, as an example, an airplane with unswept wing and tail and having the control stick fixed (i. e., elevator locked). To account for the effect of elastic deformatioft approximately, we shall take a reference section of the wing and a reference section of the tail determined in the same manner as in § 4.6.t Let the angles of attack of the wing and the tail be a„j0 and at0 respectively, when the total lift coefficient CL vanishes. If the fuselage is now rotated through an angle a about the airplane center of gravity, the new angle of attack of the wing will be (аю0 – far 9W), and that of the tail, (a(0 + a – f 0t); 6W, 6t being the elastic twisting angles of the wing and tail, respectively. 6t can be found from the equations of § 4.6. In the case of a locked elevator, we may regard the tail as a full-chord elevator and put
m = 0, a2 = at, /3 = а + а<0 from which (1)
A=qtlqm v, B=-A
To derive an expression that gives the total angle of twist of the tail as a result of the rotation a, let us add a term CMotqtStct to the right-hand side of the expression for Mt in Eq. 7 of § 4.6, to represent the moment about the aerodynamic center at zero lift. Substituting Lt and Mt from Eqs. 7 of § 4.6 into the relation
![]()

![]() (2)
(2)
 |
and solving for 0t, we obtain
where K3 denotes the spring constant for wing twisting with respect to airplane c. g., K3 is the torque required to act at the wing-reference section to produce a change of angle of attack of 1 radian at the wing-reference section with respect to a fuselage that is clamped at the c. g. Equation 4 is a slightly more general expression than Eq. 7 of § 3.1.
Neglecting the tail lift in comparison with the wing lift, we obtain the total lift coefficient of the airplane from Eq. 4:
|
|||
|
|||
|
|
||
|
|||
![]()
Solving Eq. 5 for a, and substituting into
CLt = a I a(0 + a + 01)
we obtain
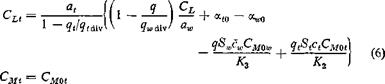
If the airplane were perfectly rigid, then qw alv and qt div are infinitely large and CLi and Cm are obtained from Eqs. 6 by putting all terms involving qw div, qt div, K2, and K3 to be zero. Therefore the change of CLt and Cm due to the elastic deformation of the airplane can be easily calculated. The total pitching moment about the airplane c. g. is, clearly from Fig. 4.11,
M = Lw(d – h) + M3W ~ Ltl + Mt (7)
or, in coefficients form,
|
|
|
|
![]()
where 8 is the distance of the airplane c. g. behind the wing leading edge, h is the location of wing aerodynamic center behind the wing leading edge, and M0w is the aerodynamic moment of the wing about its aerodynamic center. Hence, the change of the static longitudinal stability derivative due to the elastic deformation of the airplane is
А = 1 л /ЭСЦ CtqtS idCMt
3CL) cw qSw bcLJ cwqSw 5CL J
Hence,
The static longitudinal-stability derivative of an elastic airplane is therefore
(13)
From Eq. 12 it is seen that, for an aeroelastically stable airplane, the effect of elastic deformation on the static longitudinal-stability derivative depends on the relative magnitude of the divergence dynamic pressures of the wing and tail. For instance, if the wing is so rigid that |?waiv| A |<fcaiv|> while the fuselage and tail are such that qt div is positive, then a strong stabilizing effect will occur as q approaches qt div. On the other hand, if qw div is nearly equal to qtdiv or, more precisely, if qw <nJqt div = q/qt then the effect of the elastic deformation on the static longitudinal stability disappears.
The same method can be used to study the change of stabilizer “trim” due to elastic deformation of the airplane. The trim problem is, for high-speed airplanes, one of the most important factors in tail design.













