The Kutta Condition

In the lifting-cylinder case discussed in Section 4.7, the value of the circulation gen­erated in the spinning-cylinder experiment (and, hence, the lift on the cylinder) is arbitrary. The circulation depends on an external input: the rate of spin of the cylinder. Because the Kutta-Joukouski Theorem states that the lift on an airfoil is proportional to the circulation and because from experience the lift on a particular airfoil is unique for a given orientation, there must be a physical mechanism (not an external input) that specifies a unique value of the circulation about an airfoil. The flow condition to be satisfied that results in the generation of a unique value of the circulation about a lifting airfoil is called the Kutta condition. It is stated formally herein, but first the physical phenomena that establish this condition are explained by introducing viscosity into the flow model. When the flow phenomena are dis­cussed, the viscosity switch is turned “off” again and the physical behavior observed in nature is suitably incorporated into the inviscid-flow model.

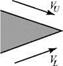
To visualize the following discussion, consider a thought experiment. A two­dimensional airfoil is set at a positive angle of attack in a viscous (real) medium at rest, as illustrated in Fig. 4.16.

The flow is started in motion to the right and rapidly brought up to a constant velocity. At the first instant of time, the flow next to the lower surface of the airfoil proceeds toward the sharp trailing edge and then around the trailing edge to the upper surface, as if there were no viscosity present. That is, the flow is essentially a potential

Figure 4.16. Airfoil started impulsively.

flow at the initial instant (Fig. 4.16a). As a consequence, this stream tube exhibits a sharp reversal of direction with zero radius of curvature right at the sharp trailing edge. This means that the velocity at the trailing edge at that instant is infinite. An infinite velocity is a physical impossibility. Because the viscous fluid cannot accom­modate this zero-radius turn, it instantaneously separates at the trailing edge and rolls up into a vortex with a counterclockwise sense (Fig. 4.16b). As the freestream velocity continues to increase rapidly, approaching a constant value, the fluid at the trailing edge continues to separate and roll up so that the instantaneous vortex grows and becomes stronger. The flow field responds to this strengthening vortex (increasing vorticity) at the trailing edge by setting up a reaction effect (circulation) about the air­foil. As a consequence, the upper-surface stagnation point, which was instantaneously located well upstream of the trailing edge, moves rapidly toward the trailing edge. Finally, when the freestream velocity reaches a constant value, the flow along the air­foil upper surface smoothly leaves the trailing edge and the fluid particles comprising the so-called starting vortex roll up tightly and are swept downstream. This starting vortex need not be included in a steady-flow problem, where the flow is considered to have been going on for a long time. The reason is that the starting vortex is located far downstream of the airfoil in such a problem and its influence at the airfoil is negligible because the velocity field associated with a vortex varies inversely with the distance.

If the airfoil angle of attack is sharply increased in a constant-velocity flow, another vortex of the same sense described previously is formed and sheds down­stream. If the angle of attack of the airfoil is suddenly decreased, a vortex of the opposite sense rolls up and sheds. The strength of the circulation around the airfoil likewise changes to a unique value as the airfoil angle of attack is changed. The experimentally observed fact, then, is that the viscous shear layer on the airfoil sur­face first rolls up at the trailing edge and then the flow field adjusts until this rollup no longer occurs. Each flow adjustment generates a unique value of circulation about the airfoil (see Section 4.10).

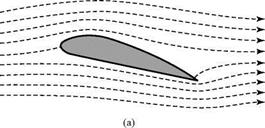
Formally, the Kutta condition states that a body with a sharp trailing edge gener­ates a circulation of just sufficient strength that the flow smoothly leaves the trailing edge. The Kutta condition has a vital role in the inviscid thin-airfoil theory devel­oped in Chapter 5 because it serves as a boundary condition.

Now, the statement that the flow smoothly leaves the trailing edge must be stated more carefully because there are two possibilities, as follows:

1. Finite trailing-edge angle.

In this case, the two velocity vectors at the trailing edge are parallel to the upper and lower surfaces. In the limit, right at the trailing edge, this implies that there are two flows going in two different directions at the same point, which is physi­cally impossible. The situation is resolved if both velocities at the trailing edge are zero (i. e., then, they have no flow direction). Accordingly, the trailing edge must be a stagnation point and the circulation must be of precisely the right
magnitude so as to move the stagnation point, which was initially on the upper surface of the lifting airfoil, downstream to the trailing edge.

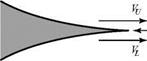2. Cusped trailing edge.

Here, there is no conflict in flow direction. However, the velocity magnitudes (upper and lower) must be identical because, otherwise, the Bernoulli Equation demands that there be a static-pressure difference between the upper and lower surface flows as they leave the trailing edge. However, between the two flows right at the trailing edge, there is a free surface (i. e., interface) that cannot sup­port a pressure difference. The conclusion is that the two velocities at the trailing edge must be the same, and a circulation is set up around the airfoil so as to make this happen. A cusped trailing edge on an airfoil is not a practical configur­ation because it requires an infinitesimal thickness. However, airfoil designers strive to come as close to this ideal configuration as possible while recalling the practical limitations imposed by structural considerations.