The Role of Large Scale Structures in Jet Noise

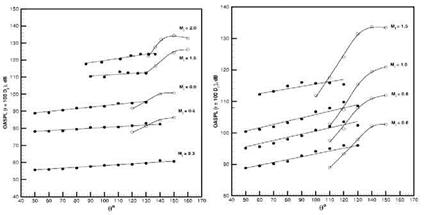
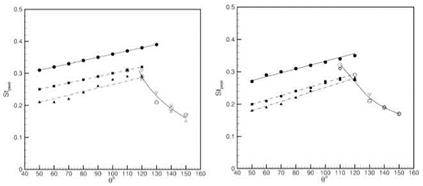
In Section 3.2 the role of large scale turbulent structures and their model­ing as instability waves was discussed. In addition, in Section 3.3 the ability of two similarity spectra to successfully collapse the measured noise spectra at all angles was described. This is only a part of a growing body of exper­imental evidence that there are two noise generation mechanisms – though this remains a very contentious issue. At issue is the role played by the large scale turbulent structures in subsonic or convectively subsonic jets. Excel­lent discussions of recent experimental evidence are given by Tam et al. (2008) and Viswanathan (2009). In particular it is noted that the noise characteristics at small angles to the jet downstream axis, including the peak noise directions, and that at larger angles to the downstream axis are very different. In addition, these differences are observed, whether the flow is subsonic or supersonic. For example, Figure 20 from Tam et al. (2008) shows the variation of the OASPL with inlet angle. The levels are deter­mined by fitting the FSS and LSS spectral shapes to the measured data. So at some angles, for example 120-140 degrees, both spectra are used to match the data. The FSS levels vary very slowly with angle, whereas the LSS lev­els increase rapidly with increase in inlet angle. Note that the effects are similar whether the flow is unheated or heated, except that in the heated case (higher exit velocity) the LSS dominates at more angles. A similar trend is observed in terms of the peak Strouhal number. This is shown in Figure 21 from Tam et al. (2008). The peak Strouhal number for the FSS noise increases slowly with increase in inlet angle, whereas the LSS peak Strouhal number decreases rapidly. Additional evidence of the differences associated with noise radiation in the two regions comes in the form of the correlations between fluctuations of velocity and density in the jet and the radiated pressure. For example, Figure 22 from Tam et al. (2008) shows the directivity of the normalized correlation between density fluctuations in

the jet and the far field pressure as a function of jet operating conditions and inlet angle. Again there is a clear demarcation of two regions: one of very low correlation at smaller inlet angles and one of very high correlation at large inlet angles. Tam et al. (2008) argue that the flow measurement, using Rayleigh scattering, is for a very small probe volume. For small or fine scale turbulent blobs, the probe will only sense the contribution from a single blob and so the correlation would be expected to be very low as many blobs would contribute to the total radiated noise. This explains the very low correlations at smaller inlet angles where the fine-scale mechanism dominates. However, though a single point measurement, the flow probe signal would be representative of larger turbulent structures that are coher­ent over a larger volume of the turbulence. The strong correlations at the larger inlet angles are consistent with the noise at these angles being radi­ated by these large scale structures. Also, though the correlation levels do decrease with at lower Mach numbers, there is still a significant correlation in the subsonic case.

As noted in Section 3.2, the large scale structures can be represented by instability waves or wave packets. There have been several recent stud­ies that have used this concept. For example, Reba et al. (2010) devel­oped a wavepacket model and determined the parameters needed to define the wavepacket (amplitude, phase velocity, and growth and decay rates) from microphone measurements on a conical cage array of near field micro-

phones. They then projected the noise associated with the wavepacket to the far field and compared with measurements. The measurements show good agreement at large inlet angles in the peak noise direction. Mor­ris (2009) examined large-scale mixing noise generation. He used the LSS spectrum to extract only the large-scale mixing noise from measured far field spectra for both subsonic and supersonic jets. From the directivities for different Strouhal numbers he was able to project back to a cylindrical surface around the jet and determine the axial wavenumber spectrum of the pressure fluctuations on the surface. He showed that the shape of the spec­trum for all the jet operating conditions was consistent with that produced by wavepackets. However, only the lowest wavenumbers (the ones that give a sonic phase velocity to a far field observer) were able to radiate in the subsonic cases. This provides further evidence that the noise radiation in the peak noise direction is controlled by the large-scale turbulent structures.