Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
The solution of the general equation
In the general case Eqn (4.22) must be solved directly to determine the function A(.) that corresponds to a specified camber-line shape. Alternatively, the inverse design problem may be solved whereby the pressure distribution or, equivalently, the tangential velocity variation along the upper and lower surfaces of the aerofoil is given. The corresponding k(.) may then be simply found from Eqns (4.19) and
(4.20) . The problem then becomes one of finding the requisite camber line shape from Eqn (4.22). The present approach is to work up to the general case through the simple case of the flat plate at incidence, and then to consider some practical applications of the general case. To this end the integral in Eqn (4.22) will be considered and expressions for some useful definite integrals given.
In order to use certain trigonometric relationships it is convenient to change variables from. v to 9, through, v = (c/2)(l – cost)), and, V| to 0|, then the limits change as follows:
9 ~ 0 —> 7Г as. y ~ 0 —» c, and
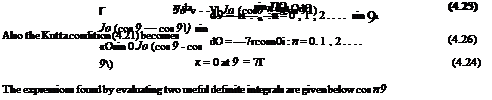
d. v = – sin 9d9
2 [15]
The derivations of these results are given in Appendix 3. However, it is not necessary to be familiar with this derivation in order to use Eqns (4.25) and (4.26) in applications of the thin-aerofoil theory.
