The thin symmetrical flat plate aerofoil

In this simple case the camber Une is straight along Ox, and dycjdx = 0. Using Eqn (4.23) the general equation (4.22) becomes

к sin 0

(cose — cos 0i)

What value should к take on the right-hand side of Eqn (4.27) to give a left-hand side which does not vary with x or, equivalently, 0? To answer this question consider the result (4.25) with n = 1. From this it can be seen that

cos 0d0

(cos0 – cos 01)

Comparing this result with Eqn (4.27) it can be seen that if к = ki = 2Ua cos 0/sin 0 it will satisfy Eqn (4.27). The only problem is that far from satisfying the Kutta condition (4.24) this solution goes to infinity at the trailing edge. To overcome this problem it is necessary to recognize that if there exists a function k2 such that

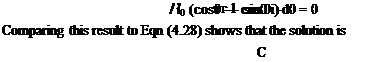then к = ki + кг will also satisfy Eqn (4.27).
Consider Eqn (4.25) with n = 0 so that

where C is an arbitrary constant.

Thus the complete (or general) solution for the flat plate is given by

The Kutta condition (4.24) will be satisfied if C = 2Ua giving a final solution of

(1 + cos 0)

sin0

Aerodynamic coefficients for a flat plate

The expression for к can now be put in the appropriate equations for Uft and moment by using the pressure:

and this shows a fixed centre of pressure coincident with the aerodynamic centre as is necessarily true for any symmetrical section.