VARIATION OF de WITH SPEED

‘’trim

When, in the absence of compressibihty, aeroelastie effects, and propulsive system effects, the aerodynamic coefficients of (6.4,13) are constant, the variation of &Нтіт with speed is simple. Then detrim is a unique function of CL for each C. G. position. Since CL is in turn fixed by the equivalent

trim trim

airspeed,! f°r horizontal flight

W

ipaV^S

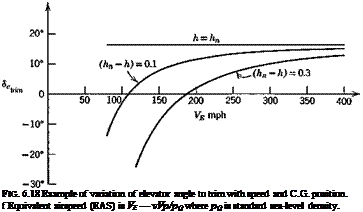
then <5etr. m becomes a unique function of vE. The form of the curves is shown in Fig. 6.18 for representative values of the coefficients.

The variation of <5„trlm with 0itrjm or speed shown on Figs. 6.17 and 6.18 is the normal and desirable one. For any O. G. position, an increase in trim speed from any initial value to a larger one requires a downward deflection of the elevator (a forward movement of the pilot’s control). The “gradient” of the movement /ЭГЛ is seen to decrease with rearward movement of

the C. G. until it vanishes altogether at the N. P. In this condition the pilot in effect has no control over trim speed, and control of the vehicle becomes very difficult. For even more rearward positions of the C. G. the gradient reverses, and the controllability deteriorates still further.

When the aerodynamic coefficients vary with speed, the above simple analysis must be extended. In order to be still more general, we shall in the

following explicitly include propulsive effects as well, by means of the parameter it, which stands for the state of the pilot’s propulsion control (e. g. throttle position), it — constant therefore denotes fixed-throttle and, of course, for horizontal flight at varying speed, tt must be a function of V that is compatible with T = D. For angles of climb or descent in the normal range of conventional airplanes L = W is a reasonable approximation, and we adopt it in the following. When nonhorizontal flight is thus included, tt becomes an independent variable, with the angle of climb у then becoming a function of tt, V, and altitude.

The two basic conditions then, for trimmed steady flight on a straight line are

L = CLyV2S = W

and in accordance with the postulates made above, we write

Grn = У> Я-)

gl = CL{a, У, іг)

Now let ( )e denote one state that satisfies (6.4,18) and consider a small change from it, denoted by differentials, to another such state. From (6.4,18) we get, for p = const, О II (6.4,20) and CLVS = const or 2VeCLe dV + V*dCL = 0 so that dOL = -2Gr — = -2GT dt lje у L>e (6.4,21) where t is defined in Table 5.1. Taking the differentials of (6.4,19) and equating to (6.4,20 and 21) we get

Gia d* + CLd dde = – GL:r dn – (CLr + 2CL) dt 4

Cmx da + cme dde = —cmir dTT-Cmydt

where CLy = дСь/дУ and Gmy = dGmjdt. From (6.4,22) we get the solution for dd, as

There are two possibilities, tt constant and tt variable. In the first case

It will be shown in Chapter 9 that the vanishing of this quantity is a true criterion of stability, i. e. it must be >0 for a stable airplane. In the second case, for example exactly horizontal flight, tt — tt(V) and the ir term on the r. h.s. of (6.4,23) remains. For such cases the gradient (ddetTimldV) is not necessarily related to stability. For purposes of calculating the propulsion contributions, the terms CL^ dir and Gmjr dir in (6.4,23) would be evaluated as dCL^ and dCm^ [see the notation of (6.3,13)]. These contributions to the lift and moment are discussed in Sec. 7.3.

Fm. 6.19 Reversal of <5trim slope at transonic speeds, тг = const.

The derivatives CLy and Gmy (see Sec. 7.8) may be quite large owing to slipstream effects on STOL airplanes, or Mach number effects near transonic speeds. These variations with M can result in reversal of the slope of <5etrlm as illustrated on Fig. 6.19. The negative slope at A, according to the stability criterion referred to above, indicates that the airplane is unstable at A. This can be seen as follows. Let the airplane be in equilibrium flight at the point A, and be subsequently perturbed so that its speed increases to that of В with no change in a or de. Now at В the elevator angle is too positive for trim: i. e. there is an unbalanced nose-down moment on the airplane. This puts the airplane into a dive and increases its speed still further. The speed will continue to increase until point G is reached, when the de is again the
correct value for trim, but here the slope is positive and there is no tendency for the speed to change any further.