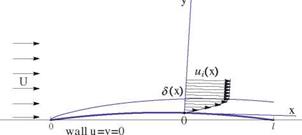
Viscous Stresses in 2-D (Cartesian Coordinates)

To account for viscous stresses in the momentum equations, consider an element as in the sketch, Fig. 8.4.

The viscous forces in the x-direction are

( Ax Ax

&1,1(x + —, y, t) – ah1(x – —, y, t) Ay

( Ay Ax

+ 02,1 (x, y + -2-, t) – <72,1 (x, y – —, t) Ax (8.13)

Dividing by Ax. Ay and taking the limit gives

д71,1 до2,1

dx + dy

Fig. 8.4 Viscous stresses in 2- D

Similarly, the viscous forces in the y-direction is

Ax Ax

01,2 (x + —, y, t) – 0-1,2(x – —, y, t) Ay

( Ay Ax

+ 02,2(X, y + —, t) – 02,2(X, y – —, t) Ax

Again, dividing by Ax. Ay and taking the limit gives

(8.16)

Note: taking moments about the centroid (x, y)

0 = ^ M = o1,2Ax. Ay – ff2,iAx. Ay

hence 01,2 = 02,1.

The momentum equations for viscous fluid flow become:

dp. do1,1 , do2,1 dx + dx + dy d p. d01,2 , do2,2 dy + + ~dy~

Similarly,
(8.24)
since
(8.25)
8.1.4 Navier-Stokes Equations for 2-D Incompressible Flows

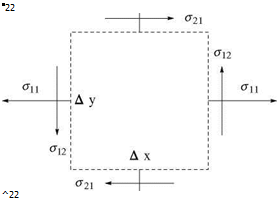
Fig. 8.5 Boundary layer development on a thin airfoil

The boundary conditions for the flow past a profile or a plate are the following (Fig.8.5):

• on the solid surface, no penetration, no slip,

• in the far field, no disturbance.