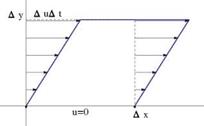
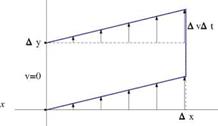
Vorticity Versus Strain Rate in 2-D

Consider a rectangular particle of initial size (Ax, Ay) near the wall y = 0. On the upper edge the velocity is u = Au. Equivalently, this corresponds to moving with a particle located at (0, 0) in a velocity field where v = 0. After a short time At the particle is sheared and takes the shape of a parallelogram. The strain rate is defined as є1і2 = limAy^0 Ay = &y. Similarly, considering a velocity field with u = 0 and upon superposition with the previous flow field, one finds the following strain rate, Fig.8.3

du dv

£1,2 = £2,1 = +

dy dx

Note: any square matrix A can be decomposed uniquely into the sum of a sym­metric and antisymmetric matrices

A = 1 (A + A*) + 1 (A – A)

where A* is the transposed of A. Hence

1 / £1,1 ё 1,2 2 £1,2 £2,2 1 ( 0 – из = 2 U 0

(8.10)

(8.11)

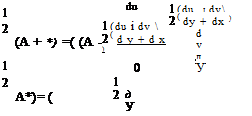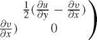
Therefore

u(x + Ax, y + Ay, t)
v(x + Ax, y + Ay, t)
general 2 – D motion

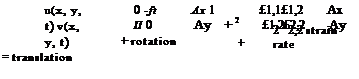(8.12)