WENO Reconstruction on Unstructured Grids

In order to compute the higher order operator for the grid cell C^ a reconstruction of the cell averages defined

(19)

is done, where |C(;) | is the length, the surface or the volume of the gird cell depend­ing on the space dimension. To ensure a stable reconstruction even at discontinuit­ies, a high order Weighted Essentially Non Oscillatory (WENO) reconstruction was chosen. This method was first introduced by Shuet al. [11,10] and Osheret al. [13]. For the proposed defect correction method, the modified reconstruction algorithm by Dumbser et al. [4] is used which ensures a robust method on 2D and 3D unstruc­tured meshes even with distorted cells [4] eliminating scaling and bad conditioning problems common to WENO reconstruction technique.

In this approach, the reconstructed polynomial is built by a linear combination of orthogonal basis functions as given in [3] for triangles in 2D and tetrahedrons in 3D. We write the reconstruction polynomial for the element C() as

with |, n and Z the coordinates in the reference coordinate system. Unlike the common WENO reconstructions at discrete cell points, the basis polynomials are continuously extended over the whole stencil and are then restricted to the considered element C^ after having obtained a reconstruction polynomial. The number of degrees of freedom L being L = {M+){M + 2) in 2D and L = (M+ 1) (M+ 2) (M+ 3) in 3D depends on the polynomial degree M of the basis functions Wl. Whereas the basis functions are space dependent, the reconstructed degrees of freedom w(i)l depend only on time.

Similar to the finite element framework, the reference space is the unit element Cu. This is a triangle with the canonical coordinates (0,0), (0,1) and (1,0) in 2D and a tetrahedron with the canonical coordinates (0,0,0), (0,0,1), (0,1,0) and (1,0,0) in 3D. The transformation from the physical space x—y — z into the reference space I — n — Z can be done by a linear transformation matrix (see [4]). To perform the reconstruction, several stencils have to be chosen which is done in the reference space. There are three groups which are defined as follows:

1. First the central stencil is built by adding successively Neumann neighbors, i. e. immediate side neighbors of the considered cell Cp), to the stencil until the de­sired number of cells ne in one stencil is reached. The size of ne will be discussed later on in this chapter.

2. The following stencils, three of them in 2D and four in 3D, are chosen out of the primary sectors. As mentioned before this is done in the reference space ц,£. So the primary sectors are spanned by the vectors starting from each vertex of the unit element Cu along the edges intersecting this vertex. Transformed elements are then successively added to the stencils.

3. As shown by Kaser and Iske [12] it is favorable to take one more family of stencils into account than the two mentioned above. Although this increases the computational effort it ensures a stable and robust reconstruction in 2D and 3D configurations for special locations of the discontinuities. Additionally it im­proves the one sided reconstruction, e. g. at walls. The so-called reverse sectors are spanned by the negative vectors of each primary sector defined above.

This sums up to ns = 7 and ns = 9 stencils in 2D and 3D which are used for the reconstruction. At the domain boundaries or for the case that not all stencils could be filled up due to geometrical reasons, the total number of stencils ns can decrease.

For a conservative reconstruction one must assure that the polynomial distribu­tion wi in each cell C^ of the stencil m conserves the integral mean value of the cell at hand C(is).

T7T—[ W(0 (IWV = «<(,-,) (21)

ІЧб) C(is)

The evaluation of the conservation condition is carried out in the reference space. This is done by applying linear transformation matrix with respect to the element C(i) to each cell in the stencil, where the transformed elements are in the following denoted by C({). Taking into account that the degrees of freedom W(i) are not space dependent, the above equation results in

/

The Jacobian determinant which is introduced due to the transformation appears on both sides of equation (22), so it cancels out and with it scaling effects are elimin­ated as well. Furthermore, Abgrall reports in [1] that ill-conditioned reconstruction matrices are also avoided through this effect.

As the transformation to canonical coordinates is only done for the reconstructed cell, the integration in equation (22) turns out to be non-trivial. This is not the case if a second transformation with respect to the reconstructed cell is done additionally. For more details see [4]. With it, the left hand side of equation (22) can again be easily integrated using the Gaussian quadrature with an appropriate accuracy. This yields the following linear system which have to be solved for the reconstructed degrees of freedom.

Aw = a (23)

For a number ne= L of elements per stencil the matrix A becomes square and easy invertible, but for realistic meshes this leads to an unstable scheme. So, to ensure the
robustness of the reconstruction we enlarge the stencils, see also [12]. The number of the elements per stencil is chosen as ne = 1.5L in 2D and ne = 2L in 3D. In addition the matrix can contain linear dependent rows due to geometrical reasons. This means that the reconstruction matrix A may not be invertible. This is avoided by adding successively new elements to the stencil if one of the singular values of the matrix becomes zero. The overdetermined system (23) can be solved by an algorithm of singular value decomposition or, as it is done in our framework, by a least-squares method with the constraint (21).

The degrees of freedom w^ are now known, so the polynomials w(j)(%, n, Z) on each stencil are known and the final nonlinear reconstruction polynomial wj™0 in the cell C(i) of degree M is defined by

Unlike the common ENO (Essentially Non Oscillatory) schemes, where only the less oscillating polynomial is chosen, all reconstruction polynomials on each stencil are taken into account by a linear combination as done in eq. (24) with the normal­ized nonlinear weights (os

S)s Xs

^=-s——— with m,= (25)

X & (Є + °s)

r=1

according to [11, 17, 4], whereas the non-normalized nonlinear weights a>s depend on the linear weights Xs and the oscillation indicators os.

The parameters є and r are set in the common range given in the literature [17,4],

i. e. є = 10-5 – 10-14 and r = 2 – 8. Thereby є is regarded as a threshold for a division by zero which does not influence much the stability of the reconstruction scheme. The parameter r states the sensitivity of the nonlinear weights relative to the oscillation indicators os. For bigger r the reconstruction procedure tends to an ENO behavior, whereas for smaller values the scheme becomes more oscillatory.

For the weights (Ds in (24) suitable oscillation indicators are necessary to ensure a robust reconstruction. In literature ([10, 12]) this is usually achieved by a scal­ing with the cell volume. As the reconstruction procedure is done in the reference coordinate system this is not necessary any more. Due to the definition of the poly­nomials (20) os can furthermore be computed in a mesh independent way

os = (v/s)T^Y/s (26)

with ws, the vector of the degrees of freedom of the polynom on the stencil m and Z the universal oscillation matrix defined by

dr

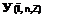щ^щ-ут, пЛ WdndC,

(27)

whereas у = r – а – в. As the reconstruction basis functions W are generally given, the oscillation matrix is neither dependent on the mesh, nor on the problem, i. e. it can be computed and stored in advance of a computation, considerably increasing the efficiency of this reconstruction method.

In contrast to the common WENO schemes the linear weights are not used for the improvement of the accuracy as was shown by Liu, Osher and Chan [13] but simply defined by

according to Dumbser et al. [4], with Xc > 1, which puts a high emphasis on the central stencil. It was shown in [4] that a choice of Xc = 102 – 105 does not show sensitivities in the results. Nevertheless, lower Xc yield better results at discontinu­ities and larger weights are favorable for smooth solutions.