A FIRST MIXED д UPPER BOUND

The j upper bound above does not account for the real nature of the parametric uncertainties, so that this upper bound is called "a complex /л upper bound": real and complex scalars are indeed treated in the same way in the structure of the scaling matrix D. An additional scaling

matrix G can take into account the specificity of scalars <S[. G must belong to:

G — {G — diag(GGmr, 0^m 0^

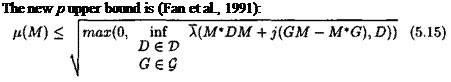with Gi = G* Є Cki’ki} (5.14)

The complex p upper bound of the previous subsection is recovered with G = 0 (see equations (5.12) and (5.13)). On the other hand, the new quasi convex and non differentiable optimization problem can be solved,

either using a general LMI solver (the issue is to minimize a maximal generalized eigenvalue), or using the specific structure of the optimiza­tion problem.

Indeed, an alternative formulation of the above mixed p upper bound was proposed in (Young et al., 1995). The following sets of scaling matrices are associated to Д (IV = 5Y=ri &i):

^ — diag(D 1,…, Dmr+mc j d Jfemr+mc+i > •

with det(Di) фО, Dte CkiM, dj ф 0 and dj Є C} g = {G = diag(gi,…,gN, Okmr+I,…,Okmt,+mc+mc) with gj Є R} (5.16)

D Є V is consequently a positive definite matrix, unlike D Є V. G Є G is an hermitian block diagonal matrix unlike G Є Q, which is a real diagonal matrix. The following Lemma is extracted from (Young et al., 1995).

1 — jG)F~^4) < 1

then p(M) < /3.

Remark: roughly speaking, the /.t upper bound proposed in the above Lemma involves the minimization of a maximal singular value, whereas the p upper bound of (Fan et al., 1991) involves the minimization of a maximal generalized eigenvalue. These bounds are nevertheless identical (Young et al., 1995): see Lemma 2..1 of chapter 10.