Arbitrary Motion

There will be two different arbitrary motions to be studied. First, we will see the unsteady aerodynamic force and moment created by the arbitrary motion of the airfoil. Afterwards, the response of an airfoil to a sharp edged gust will be studied.

3.2 Arbitrary Motion and Wagner Function

The response of the linear system to a unit step function is defined as the indicial admittance function, A(t), see Appendix 6. The response of the same system to the arbitrary excitation is given by the Duhamel integral as x(t)

t

x(t) = A(0)f (t) + J f (x)A'(f – x)Ax.

0

Let us find the indicial admittance, A(t), as the unsteady aerodynamic response of the system for the arbitrary motion of the airfoil. As a two degrees of freedom problem let the airfoil pitch about its midchord while undergoing vertical trans­lation. As is given in the previous section the equation for the chordline for a = 0 reads as

This downwash expression w can be used in Eq. 3.32a, b, for a simple harmonic motion with regarding the time derivative of the downwash as the apparent mass terms. This gives

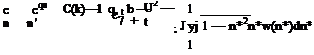ci = arm—U2 || ж*

and the quasi steady terms from 3.31a, 3.31b

2p p

cqs = (h + ckb/2 + Ua) and c^, = (h + Ua).

In Eq. 3.35a, b regarding noncirculatory terms which are the time derivatives of the vertical translation h and the angle of attack a, the coefficients become

2p Pb

c7 = C(k)(h + ab/2 + U a)+ y(h + Uck)

U U2

p pb

cm = C(k)(h + ab/2 + Ua)— y(ba/4 + Ua)

U 2U2

The first terms of both coefficients given by 3.36a, b depend on the Theodorsen function and they are valid for simple harmonic motions only. The second terms, on the other hand, are independent of the type of motion and they are just time derivatives of the vertical translation and the rotation. If we closely examine the expression in the parenthesis of the first term, (h + ab/2 + Ua), we observe that this is nothing but the expression for the negative of the downwash at the three quarter chord, i. e.,

w(b/2, t) = —(h + ab/2 + Ua).

We have seen in Eq. 3.36a, b that the circulatory terms of the aerodynamic coefficients are the function of the reduced frequency. Here, the downwash at the three quarter chord point is sufficient to find the sectional coefficients. When there is an arbitrary motion, the downwash will change arbitrarily. Since the problem is linear, we can write the Fourier components of the arbitrary downwash and superimpose the contribution of the each component on integral form to the sec­tional coefficients. For this purpose let us define the Fourier integral in the fre­quency domain

w(2; ^ = 2P J f (m)ewxdm (3.37)

— 1

Here, Дю) is the Fourier transform of the downwash and covers its full fre­quency spectrum. The inverse Fourier transform in terms of the downwash value at the three quarter chord becomes

f (x)= J, tje m‘dt (3.38)

—1

The circulatory lift at a given frequency ю can be defined as the Fourier component of the total circulatory lift. This component, on the other hand, can be written for a unit amplitude of the downwash as follows

eixt

The corresponding Fourier component for the circulatory lift at time t becomes

This component can be put into the Fourier integral

11

cci(t)=— J Accl(m, t)elx‘dm = —^J f (x)C(k)elx‘dm.

—1 —1

If we employ the same procedure for the moment coefficient, the total coeffi­cients read as

pb 1

c() = U# + Ua)—~U f (m)C(k)emtdrn

—1 і (3.39a, b)

pb 1

cm (t) = —Uji(b’a/4 + Ua)— — f (x) C(k)elxtdx

Equations 3.39a, b are applicable for the arbitrary downwash and covers piecewise continuous functions with finite Fourier transform.

Since the aerodynamic system we consider is linear, the step function repre­sentation of the downwash and the superposition technique will be applied for the aerodynamic effect of the unit change in one of the followings

(a) for a = 0, change in h,

(b) for h= 0, change in a for U = constant,

(c) for h= 0, change in U for a = constant.

Now, let us consider case (b) when U is constant the angle of attack changes from zero to a finite value ao. The downwash becomes

w(f, f) = — aoU1(f). The Fourier transform of this reads as

f(w) = —aoU J 1(f)e-ixtdf

—1

Substituting this function into the circulatory lift expression we obtain

1

cc,( f) = ao C(k)ei“fdro.

ix

—1

If we use the reduced time s = Uf/b instead of f we get

From this integral we define a new function

—1

as the Wagner function u(s), the circulatory lift coefficient becomes

cC (s) = 2naoy(s). (3.40)

The Wagner function is a time dependent function whose limit for t going to infinity approaches unity so that according to 3.40 the lift coefficient goes to 2nao-

Let us reduce the Wagner function into a numerically integrable form. If we write the complex exponential with sin and cosine terms, take the Fourier trans­form of the unit step function and consider the symmetry and antisymmetry involved in the integrands, we obtain the Wagner function in terms of the real and imaginary parts of the Theodorsen function as follows

u(s) = 2 ^-^sin (ks)dk = 1 +2 G(k)cos (ks)dk (3-41)

p k p k

0 0

For practical uses an approximate form of the Wagner function is given in BAH as

u(s) ffi 1 – 0.165e_00455s – 0.335e-03s. (3.42)

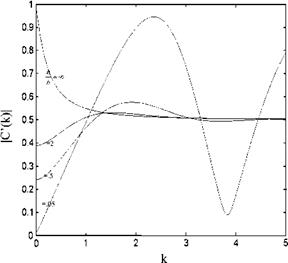
The graph of the Wagner function, based on the Jones approach and given by 3.42 is plotted in Fig. 3.11. The function at zero time takes the value of 0.5 and reaches unity at infinity. This means, after the sudden angle of attack change it takes a long time to reach the steady state value given by 3.40.

Knowing the expression for the Wagner function, we can give the unsteady aerodynamic coefficients for the arbitrary motion as functions of the reduced time in the form of Duhamel integrals.

(3.43a, b)

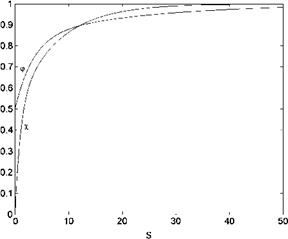We have previously seen that the Wagner function is 0.5 at t = 0. This means, the immediate lifting response of an airfoil to a sudden angle of attack change is half the lift value attained steadily. These responses are seen explicitly in the circulatory terms of 3.43a, b.

Another example for the arbitrary motion of the profile is the response to a sharp edged gust which will be studied next.