Characteristics of turbulent boundary layers

A turbulent boundary layer features small-scale, rapid, chaotic velocity fluctuations, which result in turbu­lent mixing which transports momentum across the boundary layer. This momentum transport is an apparent Reynolds shear stress, also called turbulent shear stress, and is given by Tt = pt du/dn. This adds to the molecular-motion transport which constitutes the usual laminar viscous shear stress т£ = pdu/dn, so that the total shear stress in equations (4.21) is the sum of the laminar and turbulent contributions.

( du

T{s, n) = T£ + Tt = yp + PtC, n) j —

In contrast to the laminar viscosity p which is nearly constant, the eddy viscosity pt(n) varies strongly across the boundary layer at any given location s, with the result that the turbulent du/dn profile and hence the u profile are markedly different from the laminar case. The various relevant laminar and turbulent profiles are sketched and compared in Figure 4.5.

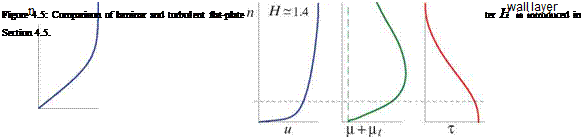Laminar

The key feature which makes turbulent boundary layers so different is that pt is large relative to p over most of the turbulent boundary layer, but falls linearly to zero over roughly the bottom 20% portion called the wall layer. Here the total stress т is approximately constant and equal to the wall shear stress tw. Hence in the wall layer du/dn varies roughly as 1/n, and therefore u(n) ~ ln n. The variation of all the quantities in the wall layer can be summarized as follows.

т(n) ~ tw ~ const.

pt (n) ~ n

т (n)/pt (n) ~ 1/n

u(n) ~ ln n

The logarithmic profile in the wall layer gives the overall turbulent profile its distinctive “knee." Its greater velocities near the wall greatly increase the turbulent boundary layer’s resistance to adverse pressure gra­dients by a factor of five or more over laminar flow, which is crucial for the lift generation capability of typical airfoils. The main drawback is that turbulent flow results in increased skin friction and profile drag compared to laminar flow, and this discrepancy increases with increasing Reynolds number. For this reason, turbulent flow is generally undesirable wherever its adverse pressure gradient resistance is not needed.

To solve the boundary layer equations (4.21) for turbulent flow, we must also simultaneously determine the entire eddy viscosity pt(s, n) field, inside and outside the wall layer. This is one of the central goals addressed by turbulence modeling, which is an enormous field (see Reynolds [10]). Covering any such models is beyond scope here. Instead, we will only discuss the general features of turbulence on boundary layer behavior, and consider only relatively simple integral turbulent calculation methods which do not need detailed turbulence models for the eddy viscosity.