Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Compressible infinite swept wing
|
For the compressible infinite swept wing, the PG transformation gives the following modified geometry,
|
Figure 8.17: Prandtl-Glauert transformation of infinite swept wing.
Applying the previously-derived incompressible solution (8.97) we have
Cl = Cta a cos Л
 |
 |
and the compressible Cl is then obtained using Gothert’s Rule and the reverse PG transformations.
|
dCL да |
~ Р ’ |
Л |
х0° (2D) |
|
dCL |
cea cos Л |
Л – |
>90° |
|
да |
sin Л ’ |
|
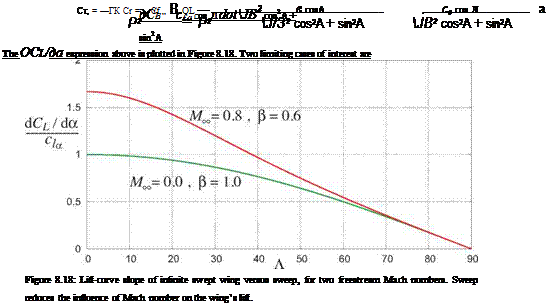
so that large sweep angles mitigate compressibility effects, as can be seen by the coalescence of the incompressible and compressible curves in Figure 8.18. |
