We now need expressions for the derivatives that appear in (4.9,18) and (4.9,19) in terms of the nondimensional derivatives. A few examples of these are derived as follows to illustrate the procedure, and the whole set needed for (4.9,17) is displayed in Tables 4.4 and 4.5. Derivatives with respect to v or /3 are usually negligible and are not included.
THE Z DERIVATIVES
THE M DERIVATIVES
These are also found in a manner similar to the Z derivatives. In this case we start with M = CmpV2Sc and note from (4.9,6) that Cmo = 0.

|
|
|
From Table 4.1, L = CtpV2S —. Hence
|
|
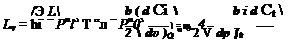 |
|
|
|
|
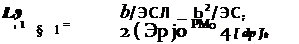 |
|
|
|
|
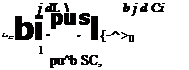 |
|
THE N DERIVATIVES
These are found in a manner similar to the L derivatives.
|
|
|
THE Y DERIVATIVES
These are also found in a manner similar to the L derivatives. In this case we start with Y = CypV2S.
|
|
|
4.12 Elastic Degrees of Freedom
In the preceding sections we have presented the “main” equations of motion, that is, those associated with the six rigid-body degrees of freedom. Now it is known that the stability and control characteristics of flight vehicles may be profoundly influenced by the elastic distortions of the structure under aerodynamic load (AGARD, 1970; Milne, 1964; McLaughlin, 1956; Rodden, 1956). Additionally, there are phenomena not primarily related to stability and control, but rather to structural integrity, in which elastic deformation is a primary element—i. e., structural divergence and flutter. In order to understand and analyze all these effects, one needs the equations that govern the elastic deformations, and as well the changes that such deformation introduces into the six main dynamical equations.
A full treatment of this branch of flight mechanics—aeroelasticity and structural vibration—is beyond the scope of this text, and the reader is referred to (Bispling – hoff, 1962 and Dowell, 1994) for comprehensive treatises on it. Here we content ourselves with presenting the framework of the analysis, but omit most of the structural
|
|

and aerodynamic details. Enough material is given, however, to show how the static and dynamic deformations are integrated into the preceding mathematical model of the “gross” vehicle motion.
The deformation analysis is almost invariably treated by a linear theory, even when the rigid-body motion is not. We shall therefore assume at the outset that the distortional motions are “small” and that all the associated aerodynamic forces are linear functions.
![]()
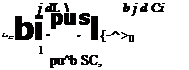
![]()











