DYNAMIC MASS BALANCING*
Since purely translational, purely rotational, and purely control-surface oscillations are stable in most cases, it is clear that a key to flutter prevention is to break up any coupling between the various degrees of freedom.
 |
Consider a two-dimensional wing of infinite torsional rigidity fitted with an aileron whose center of mass lies behind the hinge line. If this wing is initially at rest and is suddenly given an upward motion, the aileron will tend to lag behind the wing to produce a relationship as shown in Fig. 5.3.
Thus an aileron motion is induced by a vertical motion of the wing by inertia force. This is called an inertia coupling. If the aileron center of mass lies on the hinge line, the inertia coupling will vanish, but the aileron motion may still be excited by the vertical motion because a nonvanishing aerodynamic moment about the hinge line may exist. This is called an aerodynamic coupling. Finally, some elastic linkage may exist so that a vertical deflection causes the aileron to rotate, thus forming an elastic coupling. Similar terms are used for the interconnections between other degrees of freedom, t
An airplane designer has only a limited control over the elastic and aerodynamic couplings, but inertia coupling is more controllable. Since the critical flutter speed is often very sensitive to inertia coupling, a careful consideration of “dynamic mass balancing” can be very rewarding.
* Much of the concept of dynamic mass balancing is due to von Baumhauer and Koning,5-6 who, in 1923, gave results of wind-tunnel tests in which flutter had been eliminated by adding weights to the paddle balance then used for aerodynamic balance.
t A coupling between the wing and aileron can be broken by using a rigid, irreversible control system, i. e., one in which the aileron is not free to rotate.
Consider first the flexure-aileron coupling of a cantilever wing. The inertia coupling can be broken if it is possible to arrange the mass distribution in such a way that the inertia force due to bending induces no rotational moment about the aileron hinge line. An aileron with mass distribution so arranged is said to be dynamically mass-balanced with respect to flexural motion. Otherwise it is mass-unbalanced. A measure of the mass unbalance is the product of inertia of the aileron about two perpendicular axes, one coinciding with the aileron hinge line, the other corresponding approximately to the wing root.5,20 Let an aileron (Fig. 5.4) be mounted on a hinge line Y, which in turn is mounted rigidly on a wing oscillating about an axis X (assumed perpendicular to Y). The
|
Fig. 5.4. Notations for Aileron mass balance. |
inertia force acting on any element of the aileron is proportional to the amplitude of oscillation of that element. If the aileron is perfectly rigid, and the wing oscillates as a rigid body as if it were hinged about the X axis, the acceleration will be proportional to the distance y, and the inertia moment about the aileron hinge line due to an element of mass dm will be proportional to x у dm, where x is the distance of the element dm behind the aileron hinge line. Hence, the total moment is proportional to the product of inertia of the mass of the aileron:
Jxv = fay dm
where the integral is taken over the entire aileron. If Jxy = 0, the inertia coupling is eliminated for the mode of oscillation assumed. In practice, Jxy seldom vanishes. As a measure of the mass unbalance, a non – dimensional “dynamic-balance coefficient”
_________ Jxy________
Mass x area of aileron
is introduced by Roche5-3®
In a modern sense, mass balancing means the best arrangement of masses. For an airplane the location of engines, fuel tanks, radar equipment, and so on has a profound influence on the critical flutter condition.
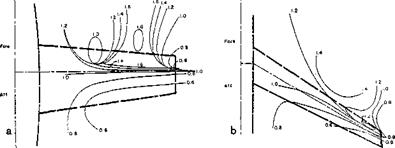
As an example, Figure 5.5 shows the results of a systematic study of the effect of engine locations on the flutter speed of airplanes with unswept and swept wings by means of an electric analog computation. A point on the contour curves of constant flutter speed represents the actual location of the center of gravity of the added mass, and the numbers shown refer to unity based on the flutter speed of the bare wing, without any added mass.
|
Fig. 5.5. Contours of constant flutter speed for (a) unswept and (b) swept tapered wing showing effect of concentrated mass location. Symmetric Flutter. (From С. H. Wilts, “Incompressible Flutter Characteristics of Representative Aircraft Wings.” NACA Tech. Note 3780.) |
Thus an engine whose center of gravity is located at a point on a contour labeled 1.4 will improve the flutter characteristics of the bare wing by raising its flutter speed by a factor of 1.4. A knowledge of such trend curves is of great value to the engineer; but such accurate information certainly cannot be given by a simple criterion. It is a general practice in airplane design to start flutter analysis at an early stage, so that certain decisions such as the location of engines and fuel tanks, etc., can be made.
Mass balancing is extremely critical for rockets and satellites. For artificial satellites the mass distribution reacts with gravity gradient and influences the guidance and control. Moving masses are employed to control the damping of a satellite. Active motion of masses makes the system nonconservative. For example, in Ref. 5.74 the author considered the stability of a spinning space station due to periodic motions of the crew. Instability may occur if the period of an astronaut’s motion bears certain ratios to the half-period of the spin of the satellite. If he moves back and forth along the radius of a circular, planar satellite, instability will occur when the period of his motion is approximately an integral multiple of the half-period of the satellite spin. A similar conclusion holds if the astronauts move with constant speed or oscillate periodically in circumferential direction. The heavier the moving masses or the larger their amplitude of motion, the wider is the region of instability.