Finding the tail load

This conclusion only applies when there is no force on the tail plane. When there is such a force the problem is slightly more complicated, but can still be solved by the principle of moments. Consider a further example –

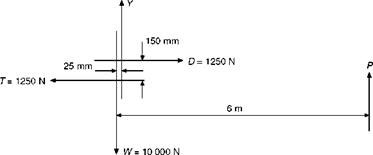
An aeroplane weighs 10 000 N; the drag in normal horizontal flight is 1250 N; the centre of pressure is 25 mm (0.025 m) behind the centre of gravity, and the line of drag is 150 mm (0.15 m) above the line of thrust. Find what load on the tail plane, which is 6 m behind the centre of gravity, will be required to maintain balance in normal horizontal flight.

Let the lift force on the main planes = Y newtons

Let the force on the tail plane = P newtons (assumed upwards)

Then total lift = L = Y + P (Fig 5.8)

But L = W= 10 000 N

:.Y+P= 10 000 N (1)

Also T = D = 1250 N (2)

Take moments about any convenient point; in this case perhaps the most suit­able point is 0, the intersection of the weight and thrust lines.

Nose-down moments about 0 are caused by Y and P

W and T will, of course, have no moments about 0,

Fig 5.8 The four forces and the tail load

So total nose-down moments = 0.025 Y + 6 P

(all distances being expressed in metres) Tail-down moment about 0 is caused by D only,

So total tail-down moment = 0.15 D 0.025 Y +6P = 0.15 D

i. e. Y + 240 P = 6 D (3)

But from (1), Y + P = 10 000

2 39P = 6D – 10 000 But from (2), D = 1250

239P = 6 X 1250 – 10 000 = 7500 – 10 000 = -2500

P = -(2500/239) = -10.4 N

Therefore a small downward force of 10.4 N is required on the tail plane, the negative sign in the answer simply indicating that the force which we assumed to be upwards should have been downwards.

The student is advised to work out similar examples which will be found in Appendix 3 at the end of the book.