Fluid Dynamic Loads

The fluid dynamic pressures and loads generated by the airfoil can be calculated by using the unsteady Bernoulli equation:

By recalling Eqs. (13.45)-(13.46), the terms inside the second parentheses become – (V0 + ft X r) = [17(f) – 0(0*1, 0, 0(0*]

If the reduced frequency (вс/U) is small and the point of interest is on the airfoil then the pressure equation becomes

n — n Дф ЭФ ЭФ

and in this case ЭФ/dz has the same value above and under the chordline and does not contribute to the pressure difference. The pressure equation thus becomes

p ox dt

where the first term is similar to the steady-state term, but for the time – dependent case also the change in the potential contributes to the pressures (due to the acceleration of the fluid).

The pressure difference across the airfoil Ap (positive Ap is in the +z direction) is then

Г ЭФ ЭФП г э э 1 Ар=Р’-Ри = 2р[Щі) — + — ] = р|и(0-ЛФ+-Дф] (13.67)

where ДФ(х, г) = Ф(х, 0+, г) – Ф(х, 0—, г) = /5 у(*0. 0 dx0 = Г(дс, г) and there­fore the pressure difference in terms of the airfoil chordwise circulation у becomes

Ap = plJ(t)Y(x, 0 + J-J y(*o.0«ko] (13.67a)

The normal force on the thin airfoil is then

L’ = Fz = j Apdx = j р[и(і)у(х, t) + pjT(x, t)] dx

= pU(t)T(t) + p f f Г(х, 0 dx Jo dt

where the first term is due to the instantaneous circulation (and similar to the steady-state circulatory term) and the second term includes the contribution of the time dependency.

To evaluate the time derivative of the velocity potential in terms of the coefficients A„ (appearing in Eq. (13.59)), recall that Ф = J q • d/ (or ДФ = Sydl)

д Э Г д Ґ c

— ДФ(х, t) = — j y(xo,

For a given airfoil geometry, the mean camberline t](x, t) is a known function and the coefficients A0(t), Ax(t), A2{t), …. can be computed by Eqs. (13.61) and (13.62) (assuming that the wake influence is known). The pressure difference of Eq. (13.67) can be evaluated since all terms in this equation depend on the coefficients An(t). The force in the z direction is then

L’ = FZ= Apdx = 2p[ (е/2(0|А)(0 1 + C-°^+ X /f„(0sin(/tfl)1 Jo Jo 1 L sin v n=i J

+ Bo(& + sin i?) + sin 20^

і B„[^” ~ Ц* – ™(M 4-1) £si" ***

“2 L 2(n — 1) 2(n + 1) JJ 2

These integrals are similar to those treated in Section 5.3 and after their

evaluation we get

L'(t) = pcj— 80 + —81 + ~ 82 + 7tU2A0 + — U2A^ (13.71)

In terms of the i4„’s (using Eq. (13.70)), we get

L’(t) = ;rpc{[t/2A0 + — (IMo)] + ‘у + (UA0 + ljt (UA*

(13.71a)

and it is clear that the velocity and the coefficients are a function of time (e. g., U = 1/(0, Ая-Ая(0).

The pitching moment about the airfoil’s leading edge is M0(t) = – jCbpxdx = – j P^WyАФ + |дф]*<*х

= -2p f f І/2(г)[ло(0 + 2 A„(0 sin (n0)l

Jo l L sin v ns) J

/0 1

+ 8O(0 + sin 0) + ~ 4 s^n

■A rsin(n-l)0 sin(n +1)011 c c. .

and after an evaluation of these integrals we get

With the use of Eq. (13.71) for L’, the moment about x = 0 becomes,

Щ0 = “PC2 | [‘у (a> + Al “ у) + ^ B° + Bl + 4 B2 ~ Jg 83] (13.72) and in terms of the A„’s,

Щ0 = – pc2f [y A, + II(£M0) + у Л, + f |(^0

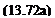и2 с д с d 1

“ +–(ВД-—-(iM3)

4 8 3r 2′ 32 ЭГ 3/J

Example 1. Small-amplitude oscillations of a thin airfoil. One of the simplest and yet important examples is the small-amplitude unsteady motion of a flat plate airfoil, which was analyzed by Theodoresen13 3 and by von Karman and Sears.13 4 For this case let us assume that the (x, z) frame of reference in Fig. 13.14 moves to the left of the page at a constant speed U(t) =U = const, in an otherwise stationary fluid. Also, the (x, z) frame does not rotate for this example

(0 = 0 = 0) and the small-amplitude unsteady motion will be introduced through the vrcl term (or the dr}/dt term in Eq. (13.55)) in the boundary conditions.

The time-dependent chordline position can be represented by a vertical displacement h(t) (positive in the z direction) and by an instantaneous angle of attack a(t) (Fig. 13.18). The chordline shape is then

t) = h — a(x — a)

where a is the pitching axis location. For simplicity, first, we shall assume that the pitching axis is at the origin (a = 0, and h is the vertical displacement of the leading edge) and r then becomes

tf = h — ax

and the vertical displacement is small (e. g., r « c). The derivatives of t] are

in

dx

where the dot denotes a time derivative. Substituting this into the downwash W(x, t) term of Eq. (13.55) we get

ЭФуу

W(x, t) = – Ua + h — ax —-—

Since the wake effect is a function of the motion history let us concentrate first on the loads due to the motion only. This portion of the downwash, W*(x, t), is then

• . c c

W*(x, t) = – Ua + h — da = —Ua + h — – dr + – dr cos &

and here x was replaced by the trigonometric variable d, using Eq. (13.58). Substituting this term of the downwash into Eqs. (13.61) and (13.62) provides the

values of the An coefficients:

ac ‘2U

The circulation due to the downwash W* can be obtained by recalling the results of Eq. (5.58):

г*(0 = I У(*. 0 dx = jicu(a0 + y)

and after substitution of the A„ coefficients the circulation becomes

Г*(г) = nc(Ua – h + led)

L*

The lift per unit span is then obtained from Eq. (13.71a):

and in terms of the displacement A and the angle of attack a, we get

L* = npUc(^Ua – h + ^ cdj + -^pc2^ (Ua – h) + ^ dj

In the derivation of this expression the downwash of the unsteady wake was not included. Theodorsen13 3 and von Karman and Sears134 showed that for a small-amplitude oscillatory motion the final result will include similar terms and the effect of the wake is to reduce the lift due to the first term in L* by a factor of C(k), which is called the lift deficiency factor. Now, if we consider the harmonic heave and pitch oscillations such that

h=ha sin (ot a = a0 sin Ш

then the lift per unit span becomes

L’ = KpUcC(k)i^Ua — h + ^cd^ + —(ua — h + ^oc^ (13.73a)

In the case when the pitch axis is moved to a location a (and also h is measured at this point), as shown in Fig. 13.18, then the lift per unit span will have a form similar to the result of Ref. 13.3:

L’ = jzpUcC(k^Ua — h + ^-^cdj +—~ j^(f/d — A) + -^dj (13.73b)

This can be rewritten as

L’ = L[ + L’2

where L[ is similar to the circulatory lift term in a steady motion and L is the lift
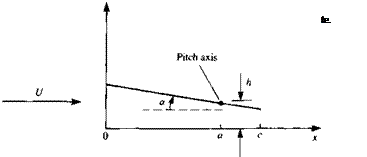
due to the acceleration, called the added mass. The lift deficiency factor C(k) is plotted in Fig. 13.19 versus the reduced frequency k, which is defined similarly to the nondimensional number of Eq. (1.52):

we 2U

As Fig. 13.19 indicates, the wake has a delaying effect on the circulatory part of the lift such that

L’x(t) = L sin (cot — w)

and m represents the time shift effect of the wake (note that m changes with the reduced frequency as shown in Fig. 13.19).

After a similar treatment of the moment about the leading edge we get

M0=-^[-^h+^a + ^c2a + UC(k)^-h + Ua+jdr]} (13.74a)

Again, when the pitch axis is moved to point a (Fig. 13.18) then the pitching moment about this point is

4a 4a

+ ——- jd

c c /

– (j – l) t/C(*)[-A + Ua + c( – *)<*]} (13.74A)

The most important portion of Theodorsen’s analysis is that the basic nature of the unsteady effect can be briefly summarized by the C(k) diagrams in Fig. 13.19. As the reduced frequency к increases, the magnitude of the pUT term in the lift is reduced. Additionally, the lift lag initially increases with the reduced frequency, but for к > 0.4 a gradual decrease in the phase shift is shown.

The above model for the small-amplitude oscillation of a thin airfoil is useful in estimating the unsteady loads in cases such as wing flutter or propulsion. The propulsion effect due to the heaving oscillations of a flat plate is shown schematically in Fig. 13.20. Recall that due to the leading edge suction the circulatory part of the lift (pUT) is normal to the instantaneous motion path, which clearly results in a propulsive (forward-pointing) com­ponent. If the heaving motion is relatively slow then the second term in Eq.

(13.73) is relatively small, too, and high propulsive efficiencies131 can be obtained.