Gust Problem, Kussner Function
The unsteady aerodynamic response of an airfoil to an arbitrary gust is going to be studied here. An airfoil under the gust load undergoes a motion which consists of arbitrary rotation about any arbitrary point and arbitrary heaving. Therefore, its behavior cannot be modeled with the downwash at the three quarter chord point. The downwash changes with respect to time and position on the airfoil as the gust impinges on. Hence, we need a new independent variable to express the downwash on the surface. This new variable depends on the free stream speed with which the gust moves on the surface of the airfoil. For this reason the downwash at the surface becomes:
Wa(x, t) =Wa(x — Ut).
The gust velocity impinging on the airfoil surface is due to the motion of the air. The downwash on the other hand has an opposite sign to that of gust. If the gust profile is given as wg then the downwash reads as
wa (x — Ut) = — wg(x — Ut).
In Fig. 3.12 the downwash distribution caused by impinging gust on airfoil surface.
As we did before, let us find the response of the airfoil to unit excitation impinging on to the leading edge as a gust at t = 0. If the constant gust speed is wo, time dependent gust function
If the gust is not simple harmonic, we have to consider all the harmonics of the gust and integrate the expressions for the aerodynamic coefficients in the frequency domain. The integral representation gives us
1
Ф) = W° J 1{C(k)[J0(k) — iJi(k)] + iJ(k)}eik(s—1) dk
—1
and
![]() 2 Ф).
2 Ф).
Now, let us relate the lift coefficient to a new function called the Kussner function as follows
Ф) = 2pUjv(s).
Here, the Kussner function is the indicial admittance for a sharp edged gust.
The Kussner function in terms of the reduced time reads as
1
v(s) = {C(k)[J0(k) — iJi (k)] + iJi(k)}eik(s—1)dk.
pi k
—1
Let us write the coefficient in the curly bracket of the above integral with its real and imaginary parts as Fg(k) + i Gg(k), and write the exponential multiplier with its sin and cosine components, the unilateral integral then reads as a real function of s
v(s) = 2 [F,(k) — Gg(k)]sin(ks)sjnkdk. (3.44)
p k
0
The approximate and convenient form of 3.44 function becomes
v(s) ffi 1 — 0.5e—013s — 0.5e—s. (3.45)
The Kussner function now can be interpreted as the indicial admittance of a sharp edged gust and can be implemented in the Duhamel integral to obtain the responses as the unsteady aerodynamic coefficients expressed in reduced time s,
s
2p,
Ф)= U wg(r)V(s — r)dr] (3.4-ба)
0
and
cm (s)=2 Ф). (3.46b)
In Fig. 3.11, also shown is the graph of Kussner function which changes more rapidly in time as compared to Wagner function.
There are two other gust problems which are going to be considered here. These are: (i) sinusoidal gust and, (ii) moving gust problems.
(i) Sinusoidal gust, Sears function: Here, the gust acting on the profile is
assumed to change sinusoidially with respect to time and space. The gust intensity with amplitude wo and frequency xg has the functional form
Wg (x, t)=w0ei2KSi (t-U)
Here, k is the wave length of the gust. For the sake of convenience, we choose the form the gust such a way that at the midchord it starts with a zero effect, i. e.,
wg (t) = woelkgt
If we let kg = 2 p U/k to be the frequency of the gust, the lift coefficient in terms of the Theodorsen and Bessel functions
ci(kg, t) = 2pU°fc(k)[Jo(k)- iJ1 (k)] + iJ (k)}elkgt
A new function, the Sears function, can be defined as
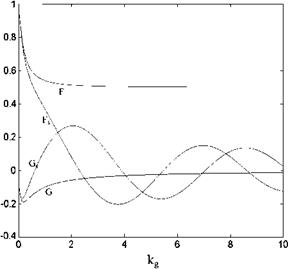
S(kg) = C (kg )[Jo (kg)- 1J1 (kg)] + 1J1 (kg) = F + lGs
whose graph is shown in Fig. 3.13. The corresponding lift coefficient then reads
 |
 |
ci (kg; t)=2pUs(kg)eikgt •
(ii) Moving gust problem, Miles functions. Here, we consider the effect of a gust moving with speed of Ug against or in the direction of free stream speed U. The resulting indicial admittance is the Miles function which is given in terms of a ratio
U + Ug
This function has a significance in rotor aerodynamics. There is a sufficient amount of information about this function and its implementations in Leishman. The parameter k takes the value between 0 and 1. When the gust speed is zero k becomes unity and the Miles function becomes Kussner function. On the other hand, for very large gust speeds k approaches zero and Miles function behaves like Wagner function (Fig. 3.11).
We have given, in summary, some analytical expressions involving the Wagner and the Kussner functions. Let us now look at another application for which a ‘time varying free stream problem’ is considered. This problem can be used to model the unsteady aerodynamics for the forward flight of a single helicopter blade.
Example 5 A rotating blade in a forward flight is modeled at its section with a sinusoidally varying free stream speed under constant angle of attack. Obtain the unsteady variation of the sectional lift coefficient in terms of the quasi steady lift coefficient and plot its variation by time for different intensities of the changing sinus term.
 |
Solution: We can write the sinusoidally varying free stream speed at a section with U(t) = Uo (1 + k sin mt). The formulae 3.43-a, b for the arbitrary motion can be used to obtain the sectional coefficient as follows
s
pb • 2p
Ф) = UUa + U[U(s)a0/2 + U(r)aoU0(s – r)dr]
0
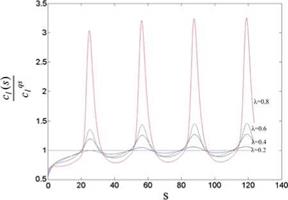
For k = 0.2 and k = 0.2,0.4,0.6,0.8 values of the ratios of the unsteady sectional lift coefficient to quasi steady coefficient are plotted with respect to time (Fig. 3.14).
The plots are obtained for four period of free stream starting at zero time. The intensity of the change in the free stream causes peaks at the lift coefficient. In each plot, there is a transition period after the onset of the motion.
As observed from the graphs the difference between the minimum and maximum of these curves increase with increasing k.











