Low-speed infinite swept wing

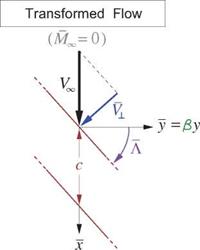
We will now investigate the lift characteristics of an infinite swept wing. The incompressible case will be considered first, followed by the compressible case treated via the PG transformation in the next section.

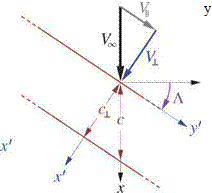
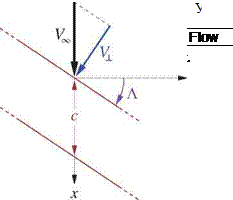
An infinite wing with sweep angle Л and streamwise chord c is shown in Figure 8.16. The angle of attack а is defined along the x-axis as usual, and hence it also appears in the streamwise section.

Figure 8.16: Lift of infinite swept wing is determined entirely by geometry and velocity in perpen­dicular x’z’-plane section.

‘ dv’ <* w +

Consider the flow as described in the rotated x’, y’, z’ coordinates where y’ is along the wing, and the x’z’- plane is perpendicular to the wing. Since each y’ location is the same, we must have d()/dy’ = 0 for all flow-field quantities. The inviscid y’-momentum equation is then

which implies that v’ is everywhere constant, and equal to the wing-parallel freestream component

v'(r) = VL єіпЛ = V (8.90)

so as to match the freestream. The continuity and remaining x’, z’-momentum equations are

d pu	‘ d pw’	= 0
dxf	dz’
‘ du’	‘ du’	dp	(8.91)
PUM	+ a?	dx’
dw’	‘ dw’	dp
PUd:¥		~d^

which describe potential 2D flow in the perpendicular x’z’-plane. Specifically, the velocities and pressure fields have the form u’, w’,p'(x’,z’), and depend only on the projected airfoil shape, chord, freestream veloc­ity, and angle of attack, all denoted by the ()l subscript.

c±	= c cos Л	(8.92)
Vl	= VL cosЛ	(8.93)
a±	= а/ cosЛ	(8.94)

And since the pressure field depends only on these parameters, the lift must also, with the spanwise V velocity being irrelevant.

Assuming a± is defined from the airfoil’s zero-lift line, the incompressible 2D-section lift is

dL = pV? c*aa±dS (8.95)

where в£а ~ 2n is the 2D lift-curve slope, and dS = c± dy’ = c dy is an element of wing area on which the element of lift dL acts. The total lift is then

= pV? cta a±_ S

= ^p(Ko cosA)2 C£a (a/cos A) S (8.96)

= c£a a cosA (8.97)

= c£a cosA (8.98)

so that sweep reduces the lift by the factor cos Л relative to an unswept wing at the same a.