Nondimensional System

The reader will already be familiar with the great advantage of using nondimensional coefficients for aerodynamic forces and moments such as lift, drag, and pitching mo­ment. In this way the major effects of speed, size, and air density are automatically accounted for. Similarly we need nondimensional coefficients for the many deriva­tives—Xu and so on—that occur in (4.9,18 and 4.9,19). Unfortunately, there is no universally accepted standard for these coefficients, although attempts have been made to devise one (e. g., ANSI/AIAA, 1992). The student, and indeed the practising engineer, should be sure to note carefully the exact notation and definitions employed in any reference material or data sources being used. The notation and definitions used in this book are essentially the NASA system, which is widely used.

Before presenting this system, we digress briefly to a dimensional analysis of the general flight dynamics problem. This helps to provide insight into what the true un­derlying variables are, and provides a basis for what follows. Imagine a class of geo­metrically similar airplanes of various sizes and masses in steady unaccelerated flight at various heights and speeds. Suppose that one of these airplanes is subjected to a disturbance. After the disturbance, some typical nondimensional variable 77 varies with time. For example, тг may be the angle of yaw, the load factor, or the helix angle in roll. Thus, for this one airplane, under one particular set of conditions we shall have

77=/(f) (4.10,1)

Let it be assumed that this equation can be generalized to cover the whole class of airplanes, under all flight conditions. That is, we shall assume that 77 is a function not of t alone, but also of

n0, p, m, l, g, M, RN

where m is the airplane mass and / is a characteristic length. Instead of (4.10,1), then, we write

7Г = f(u0, p, m, /, g, M, RN, t) (4.10,2)

Buckingham’s 77 theorem (Langhaar, 1951) tells us that, since there are nine quanti­ties in (4.10,2) containing three fundamental dimensions, L, M, and T, then there are 9-3 = 6 independent dimensionless combinations of the nine quantities. These six so-called 77 functions are to be regarded as the meaningful physical variables of the equation, instead of the original nine. Two systems of the same class are dynamically similar when all the 77 functions of one are numerically equal to those of the other. By inspection, we can easily form the following six independent nondimensional combinations:

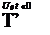m

tt, M,RN, —r, Pi

Following the 77 theorem, we write as the symbolic solution to our problem

The effects of the six variables m, p, l, g, u0, and t are thus seen to be compressed into the three combinations: m/pl3, u^/lg, and u0t/l. We replace l3 by SI, where S is a char­acteristic area, without changing its dimensions, and denote the resulting nondimen­sional quantity m/pSl by рь. The quantity l/u0 has the dimensions of time and is de­noted t*. The quantity u20llg is the Froude number (FN). Equation 4.10,3 then becomes

гг = /(M, RN, FN, p,, t/t*) (4.10,4)

The significance of (4.10,4) is that it shows 77 to be a function of only five vari­ables, instead of the original eight. The result is of sufficient importance that it is cus­tomary to elaborate on it still further. Since pt is the ratio of the airplane mass to the mass of a volume SI of air, it is called the relative mass parameter or relative density parameter. It is smallest at sea level and increases with altitude.

The main symbols for which nondimensional forms are wanted are listed in Table 4.1. The nondimensional item in column 3 is obtained by dividing the corre­sponding dimensional item of column 1 by the divisor in column 2. In the small-dis­turbance case, v and w are aerodynamic angles, for then

V = [(«о + Дм)2 + v2 + w2)]1/2

From (1.6,4)

ax = tan-‘(w/m) = tan~'[w/(M0 + Дм)]

To first order in v, w, and Дм these are

V — u0 + Au
w

ar— — = w
u0

Table 4.1 The Nondimensional System (1) (2) (3) Dimensional Quantity Divisor— General Case Divisor— Small – Disturbance Case Nondimensional Quantity X, Y, Z ipV2S ІpV2S c„ Cy, Cz mg lpV2S 1 pv2s Cw M kpV2Sc hpV2Sc cm L, N pV2Sb pV2Sb Ch c„ U, V, w V u0 u, v, w (1) a, q 2 Vic 2 ufc a, q A p, r 2 V/b 2ufb hp, f m pSc/2 pSc/2 p T pS(c!2f pS(c/2f . Ь- ^zx pS{b/2f pS(b/2)3 IX’ 1Z’ 1 zx t — t* = c/(2u0) і Note: (1) p and Да are used interchangeably with 0 and w, respectively, in the small disturbance case.

Table 4.2 Longitudinal Nondimensional Derivatives Cx cz Cm й cXu CU cm„ a CXa C- cma я cx xq cm m4 a C„ c._. r

and similarly

, v v

ft = sin — = —— = V

V u0