Potential der tragenden Flache

7.241 Geschwindigkeitspotential. Das induzierte Geschwindigkeitsfeld des Wirbelsystems eines Tragfliigels laBt sich auch mit Hilfe eines raumlichen Ge – schwindigkeitspotentials Ф(х, у,х) angeben, wie in Кар. 2.34 ausgefiihrt wurde. Dabei erhalt man den Geschwindigkeitsvektor to = u v Iw aus № = grad Ф und somit:

дФ дФ дФ

дх 9 ду ’ dz

d2Ф(x, y, z;x’, y’)

Fiir einen Hufeisenwirbel der Spannweite dy’ und der Wirbelstarke dT — k(x y’)dx’9 welcher sich am Ort x уz’ = 0 befindet (Abb. 7.15) und dessen freie Wirbel in Richtung der positiven я-Achse verlaufen, lautet der Beitrag zum Geschwindigkeitspotential nach [73]:

mit

r=i{x – x’Y + (y – y’Y + *2. (7.49)

Die Integration liber die mit Hufeisenwirbeln dieser Art belegte tragende Flache ergibt

s

Ф(х, у, z) = —f ——– —– ^ 2 ■ G(x, y, zy’) dy’ (7.50)

J (У — У )* + г2

— s

mit

xhi. y’)

G(x, y, z; y’) = f lc(x’, y’) ll + X~X ———————- dx’. (7.51)

J У (ж — x’Y + (у — у’)2 + z2 I

Xv{V’)

Dieser Ausdruck flir das Geschwindigkeitspotential der tragenden Flache wurde in ahnlicher Form bereits frliher von Th. v. Karman und J. M. Burgers [32] [33] 9 angegeben, vgl. hierzu [73].

Auf der tragenden Wirbelflache und in der freien Wirbelflache hinter dem Fliigel ist das Potential unstetig. Es besitzt, wie die nahere Untersuchung zeigt, einen Sprung beim Durchgang durch die Wirbelflache von der Ober – zur Unter – seite. Dieser ist

auf der tragenden Flache [xv(y) < x < xh(y)]:

Ф0(х’ у) — фи(х7 у) = f k(x y) dx’ (7.52a)

x„Uj)

und in der freien Wirbelflache [x > xh(y)]:

Xh(v)

фоіх. у) — фи(х’ у) = j 4х’, у) dx’ = Г (у).

Xv{y)

(*

Beim Ubergang von der tragenden Flache zur tragenden Linie ergibt sich in Ana – logie zu Gl. (7.44a) die Funktion G in Gl. (7.50) zu:

Sehr weit vor und sehr weit hinter dem Fliigel geht die Funktion G nach den Gin. (7.51) und (7.53) iiber in

Xh(v’) G(oo, г/, z; y’) = 2 f k(x y’) dx’ = 2Г(у’), xv{y’)	(7.54a)
G(—oq9 y9 z; y’) = 0.	(7.54 b)
Setzt man Gl. (7.54) in (7.50) ein, so wird:
Ф(оо, у, z) = 2 Г Г(у,) dy’, ‘ ,y’ ’ 2л J (У-У’)2 + * -8	(7.55a)
<P(—oo9y9z) = 0.	(7.55b)
Zn

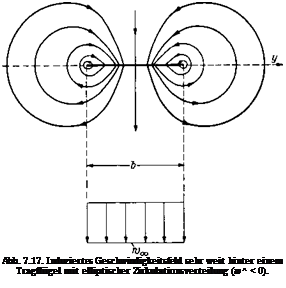
Gl. (7.55 a) stellt das zweidimensionale Potential des induzierten Geschwindigkeits – feldes in der у, z-Ebene sehr weit hinter dem Fliigel dar (Potential in der Trefftzschen Ebene [72]). Fiir die in Кар. 7.1 behandelte elliptische Zirkulationsverteilung ist das Stromlinienbild dieses induzierten Geschwindigkeitsfeldes in Abb. 7.17 dar-

ay 82<p _ Q dx2 dy2 dz2 erfhllt. Bildet man aus Gl. (7.56a) den Vektor grad <p, so stellt dieser eine Beschleuni – gung b dar:

i(x – x’)2 + (y — y’)2 + z2′

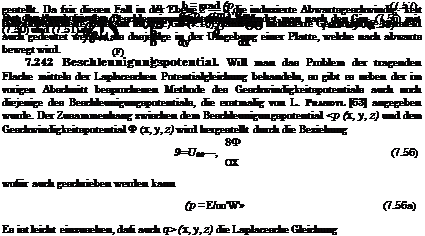Dabei ist die Integration iiber die tragende Flache zu erstrecken.[5] Auf der tragen­den Flache ist das Beschleunigungspotential ebenso wie das Geschwindigkeits­potential unstetig. Der Sprung des Beschleunigungspotentials auf der tragenden Flache betragt

<Po(x> У) ~ <Pu(x> У) = Uoq[u0(x, y) – uu(x, y)] = Ucok(x, y). (7.58a)

In der hinter dem ^liigel abgehenden freien Wirbelflache ist dagegen der Sprung des Beschleunigungspotentials gleich Null:

Po(*> У) – <Pu(x> У) = °* (7.58b)

Die letztere Tatsache bringt bei der Auffindung von Losungen mathematisch erhebliche Vorteile gegeniiber der Losungsmethode mittels des Geschwindigkeits – potentials. Aus Gl. (7.58a) erkennt man unter Beachtung von Gl. (7.41), daft der Sprung des Beschleunigungspotentials dem Druckunterschied zwischen Unter – und Oberseite der Tragflache proportional ist.

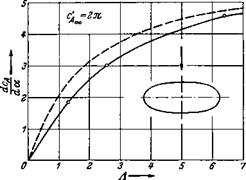
Die Methode des Beschleunigungspotentials wurde fur die Kreisscheibe von W. Kinner [37] und fiir die elliptische Flache von K. Krienes [40] angewendet. Als Ergebnis dieser Untersuchungen ist in Abb. 7.18 der Auftriebsanstieg der

Abb. 7.18. Auftriebsanstieg der elliptischen Tragflache in Abhangigkeit vom Seitenverhaltnis. ———- Einfache Traglinientheorie nach Gl. (7.29); cA ^ = 2л; — о — Tragfl&chentheorie nach Kinner [37] und Krienes [40].

elliptischen Tragflache in Abhangigkeit vom Seitenverhaltnis dargestellt. Fur die Kreisscheibe gilt nach Kinner dcA/d(x = 1,82. Zum Vergleich mit der Trag­flachentheorie ist die einfache Traglinientheorie nach Gl. (7.29) eingetragen. Die Tragflachentheorie ergibt fur alle Seitenverhaltnisse einen kleineren Auftriebs­anstieg als die Traglinientheorie. Der Unterschied beider Theorien ist bei kleinen Seitenverhaltnissen erwartungsgemaB groBer als bei groBen Seitenverhaltnissen.