Power to the Prop

The power output of a piston engine is found by coupling the engine to a test-bed dynamometer. The device measures the torque or turning force of the engine crankshaft in pounds – foot (not to be confused with foot-pounds of work). The torque in pounds-foot can be converted mathematically into brake horsepower by the following formula:

= 2п х torque х RPM BHP = 33,000

The word ‘brake’ as in brake horsepower is taken from the dynamometer’s alternate name of ‘Prony brake’. In practice, the BHP is given to indicate the power of a piston engine. Manifold pressure and RPM are selected by the pilot to produce a required percentage of BHP. For turboprops the term used is shaft horsepower (SHP) or equivalent shaft horsepower (ESHP) if the jet exhaust produces some propulsive thrust.

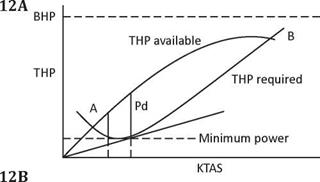
The maximum BHP for the engine can be plotted on a graph as shown in Diagram 12, Thrust & Power Curves. These are the performance curves familiar to all students of aerodynamics.

The maximum BHP is considered here to be a constant, but the BHP produced at any given time does vary under the constraints of increased altitude, temperature, power settings and supercharging. Power is the rate of doing work; that is, force or thrust times velocity.

The thrust horsepower available curve is plotted on the graph against KTAS after multiplying the BHP by the propeller efficiency. The THP will never be as great as the BHP due to the prop’s deficiencies. The performance curves for the THP available, unlike the straight BHP available curve, increases steeply up to the prop’s design speed and then reduces again to indicate the propulsive efficiency variation with increasing KTAS. The thrust horsepower required curve is the power required to equal the aircraft’s aerodynamic drag. This curve is calculated for various speeds and plotted after being calculated from the following formula:

T = drag (lbs) x velocity factor

drag x velocity x 60
33,000

Where Thrust = prop thrust in lb Velocity = FPS, MPH or knots 550 = factor for FPS 375 = factor for MPH 325 = factor for knots

An inspection of Diagram 12A, The Thrust & Power Curves, reveals various aspects of the aircraft’s performance parameters. Points ‘A’ and ‘B’ on the THP curve shows the minimum and maximum speeds for straight and level flight respectively. The line ‘Pd’ represents the maximum power differential, or the ‘excess thrust horsepower’ which produces the greatest rate of climb. A propeller is designed to be most
efficient at the aircraft’s design cruise speed. Above and below the design cruise speed the prop’s thrust and efficiency deteriorate. If the thrust were constant, then the aircraft would achieve its maximum rate of climb at the minimum horsepower required speed, but due to the loss in propeller efficiency, the maximum rate of climb is slightly higher than the minimum power speed.

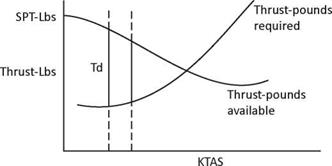
Moving on to Diagram 12B, shows the curve for ‘thrust – pounds available’ from the propeller and the second curve represents the ‘thrust-pounds required’ to equal the aircraft’s drag. The prop’s thrust is at a maximum at full engine power and zero forward velocity and decreases as the aircraft accelerates. At zero forward speed the thrust is known as ‘static prop thrust’ measured in pounds (SPT-lbs, on the diagram) when referring to a piston-engine and turboprop aircraft, as opposed to ‘static thrust’ when referring to jet engines. The prop produces on average between 2-6 pounds of static prop thrust per BHP. On the thrust-pounds curve (Diagram 12B) the line ‘Td’ represents the maximum thrust differential available from the propeller, as opposed to the maximum excess thrust horsepower shown in Diagram 12A. Notice this speed is slightly lower than that for maximum rate of climb and at this speed the maximum angle of climb will be achieved.

Using the figures given previously for a fictitious aircraft, the thrust horsepower can be found mathematically at the design cruise speed, followed by an alternate method to find the prop’s efficiency. Given the engines maximum power of 200 BHP and a prop efficiency of 84% the THP available can be calculated:

THP available = BHP x prop efficiency = 200 x 0.84 = 168 THP available

With the THP and BHP now known, the alternate method to find the prop efficiency is given as:

The propeller’s efficiency is expressed as a percentage of the ratio of power output to power input. The input is the BHP delivered from the engine to the prop and the output is the thrust horsepower delivered by the propeller. The formulas required for the BHP and THP were given earlier in this section. The thrust force delivered by the prop is found from the next formula:

Thrust = CTpN2D4

Where CT = thrust coefficient p = air density N = RPM

D = prop diameter

The power required from the engine to turn the propeller is found from the next formula:

Power = CPpN3D5

Where CP = power coefficient p = air density

N = RPM

D = prop diameter

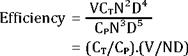From the above thrust and power formulas a further method can be used to find prop efficiency after cancelling air density

If these formulas are too complex, it can be simplified by a more straight forward formula. It has already been established the ratio of thrust horsepower to brake horsepower equals the prop’s efficiency. In addition, thrust power is thrust-force pounds times the aircraft’s speed in feet per second, or simply, TV ft-lbs/second. The power required to turn the propeller is BHP times 550 ft-lbs/second. This simplifies the propeller efficiency formula to:

Power output TV Efficiency = =

Power in P

Where T = thrust-force in pounds (or kg)

V = aircraft speed in FPS (or m/s)

P = BHP x 550 ft-lb/second (or joules)

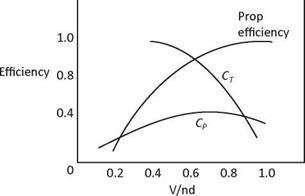
Diagram 13, Thrust & Power Coefficients, shows the thrust & power coefficients (CT & CP respectively) plus prop efficiency plotted against V/ND. The thrust and power coefficients could be plotted against angle of attack, but being a variable quantity it is more convenient to plot against V/ ND. These types of graphs for a family of props are plotted by

the propeller manufacturer to determine the values of thrust and power coefficients for any given value of V/ND. Note the curve for Efficiency versus V/ND in Diagram 13, is the same as that included in Diagram 10, Efficiency v. TAS. In conclusion, the propeller’s efficiency can be found from various formulas, depending on which factors are available for the calculations.