Radiometric Calibration of Camera

Since PSP and TSP are based on radiometric measurements, a CCD camera used for measurements should have a good linear response of the electrical output to the scene radiance. However, there are many stages of image acquisition that may introduce non-linearity; for example, video cameras often include some form of ‘gamma’ mapping. When the radiometric response function of a camera is known, the non-linearity can be corrected. Here, a simple algorithm is described to determine the radiometric response function of a camera from a scene image taken in different exposures. First, we define I( x) as a linear radiometric response to the scene radiance and m[I( x)] as the measurement of I( x) by camera electronic circuitry that may produce a non-linear electrical output. Actually, the measurement m[I( x)] is the brightness or gray level of an image, where x is the image coordinates. The non-dimensional response function relating I( x ) to m[ I( x )] is defined by

I( X )/Im«x = f[fa( X )]

where fa( x) = m[I( x)] / m( Imax ) is the non-dimensional measurement of I( x) normalized by the maximum value and Imax corresponds to the maximum radiance in the scene. Recovery of f (fa) is the task of the radiometric calibration of a camera.

Two images of a scene are taken in two different exposures. According to the camera formula (Holst 1998), I( x) is proportional to the integration time tINT and inversely proportional to the square of the f-number F. Thus, we have the following functional equation for f (fa),

f fa )/f(fa2) = R12, (5.9)

where the subscripts 1 and 2 denote the image 1 and image 2, and the factor R12 is defined as

Since m( Imax) corresponds to Imax, the boundary condition for f (fa) is f (fa = 1) = 1. We assume that f (fa) can be expanded as

f (fa)= X cjn(fa), (5.11)

n=0

where the base functions <j)n(fa) are the Chebyshev functions although other orthogonal functions and non-orthogonal functions like polynomials can also be used. Substitution of Eq. (5.11) to Eq. (5.9) leads to the following equations for the coefficients cn

S Cn[^>n(fa1) – R12 Фп ( fa2 )] = 0 ,

n=0

X СпФп(1) = 1

n=0

For selected M pixels in a scene image, Eq. (5.12) constitutes a system of M+1 equations for the N+1 unknowns cn (M > N ). For a given R12, a least-squares solution for cn can be found. In practice, since the factor R12 is not exactly known a priori, we use an approximate value of R12

An iteration scheme can be used to give an improved value of R12. Figure 5.6 shows two images taken by a Cannon digital still camera (EOS D30) at two

different f-numbers of F = 4.0 and F = 5.6, where Ansel Adams’ photograph of Mirror Lake of Yosemite was used as a test scene providing a broad range of the gray levels for radiometric calibration. Figure 5.7 shows the radiometric response function of the camera retrieved from the two images, where six terms of the Chebyshev functions in Eq. (5.11) were used. The response function of the Cannon digital still camera exhibits a non-linear behavior; it is also different for the red, green and blue (RGB) color channels.

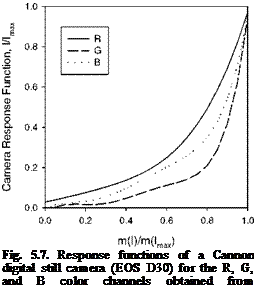Fig. 5.6. Two images of Mirror Lake of Yosemite (Ansel Adams 1935) taken by a Cannon digital still camera (EOS D30) at different F-numbers (a) F = 4.0 and (b) F = 5.6 for radiometric calibration of the camera