Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Recurrent Neural Networks
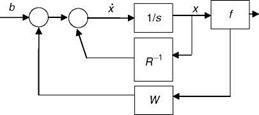
Recurrent neural networks (RNNs) are NWs with feedback of output to the internal states [19]. RNNs are more suitable for the problem of parameter estimation of linear dynamic systems, than FFNNs. RNNs are dynamic NWs that are amenable to explicit parameter estimation in state-space models [4]. Basically RNNs are a type of Hopfield NWs (HNN) [19]. One type of RNN is shown in Figure 2.18, the dynamics of which are given by [20]
xi(t) = —Xi(t)R 1 + ^2 wybj(t) + Ьг; j = 1,…, n j=i
|
FIGURE 2.18 A block schematic of RNN dynamics. |
b = f(x), (6) R is the neuron impedance, and (7) n is the dimension of neuron state. FFNNs and RNNs can be used for parameter estimation [4]. RNNs can be used for parameter estimation of linear dynamic systems [4] (Chapter 9) as well as nonlinear time-varying systems [21]. They can also be used for trajectory prediction/matching [22]. Many variants of RNNs and their interrelationships have been reported [20]. In addition, the trajectory matching algorithms for these variants are given in Ref. [22]; these algorithms can be used for training RNNs for nonlinear model fitting and related applications (as done using FFNNs).
