SYMMETRIC WING WITH NONZERO THICKNESS AT ZERO ANGLE OF ATTACK

Consider a symmetric wing with a thickness distribution of rj,(x, у) at zero angle of attack, as shown in Fig. 4.4. The equation to be solved is

У2Ф = 0 (4.29)

Here the subscript is dropped for simplicity. The approximate boundary condition to be fulfilled at the z = 0 plane is

Tp (*, У, 0±) = ± Tp G« (4- 30)

az dx

The solution of this problem can be obtained by distributing basic solution elements of Laplace’s equation. Because of the symmetry, as explained in Chapter 3, a source/sink distribution can be used to model the flow, and should be placed at the wing section centerline, as shown in Fig. 4.5. Recall that the potential due to such a point source element a, is

—a 4 nr

where r is the distance from the point singularity located at (jc0> Уо, Zo) (see Section 3.4)

r = V(x – JC0)2 + (y – Уо)2 + (z – Zo)2 (4.32)

Now if these elements are distributed over the wing’s projected area on the x-y plane (zo = 0), the velocity potential at an arbitrary point (x, y, z) will be

	(4.33)

Note that the integration is done over the wing only (no wake). The normal velocity component w^x, y, z) is obtained by differentiating Eq. (4.33) with respect to z:

. _ ЭФ _ z f q(*0, y0) dx о dyо

w{x, y,z) 4л Jwing [(x – x0)2 + (y – y0)2 + z2]3/2

n<

FIGURE 4.4

Definition of wing thickness function i at an arbitrary spanwise location y.

FIGURE 4.5

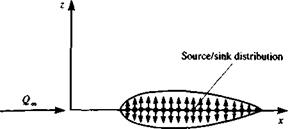Method of modeling the thickness problem by a source/sink distribution.

To find w(x, y, 0), a limit process is required (see Section 3.14) and the result is:

w(x, y, 0±)= lim w(x, y, z) = ± °^X’ ^ (4.35)

z—►0± /

where + is on the upper and — is on the lower surface of the wing, respectively.

This result can be obtained by observing the volume flow rate due to a Ax long and Ay wide source element with a strength a(x, y). A two – dimensional section view is shown in Fig. 4.6. Following the definition of a source element (Section 3.4) the volumetric flow 2 produced by this element is then

2 = o(x, y) Ax Ay

But as dz-*0 the flux from the sides becomes negligible (at z = 0±) and only the normal velocity component w(x, y, 0±) contributes to the source flux. The above volume flow feeds the two sides (upper and lower) of the surface element and, therefore 2 = 2w(x, y, 0+) Ax Ay. So by equating this flow rate with that produced by the source distribution,

2 = 2w(x, y, 0+) Ax Ay = o(x, y) Ax Ay

we obtain again

w(x, y, 0±) = ±^p2 (4.35)

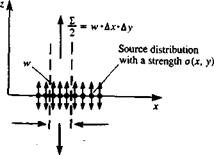FIGURE 4.4

Segment of a source distribution on the z = 0 plane.

Substituting Eq. (4.35) into the boundary condition results in

— (X у 0±) = ±^Q =±a{x’y) gz(x, y,v±> ± dxu„ ± 2

or

a(x, y) = 2Q^(x, y)

X’y’ 2 2я Jwing V(* – x0)z + (у – Уо)2 + Z2 dV,(x0, Уо), u{x, y, z) = JZ [ ZJt Jwil

[(* – X0)2 + (y – Уо) + z2]312

So in this case the solution for the source distribution is easily obtained after substituting Eq. (4.36) into Eq. (4.33) for the velocity potential and differentiating to obtain the velocity held:

The pressure distribution due to this solution will be derived later, but it is easy to observe that since the pressure held is symmetric, there is no lift produced due to thickness.